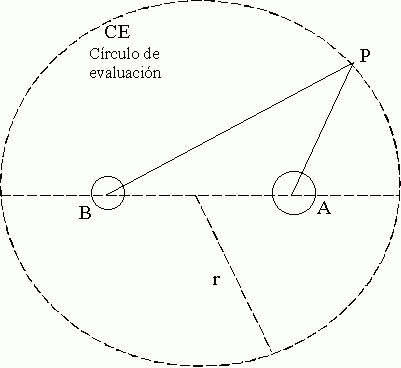
Cálculo de una Gravitación tipo Le Sage (en 2 dimensiones).

Fig SG-1
Nota: Al final de esta página se ha incluido un sumario de las constantes y variables usadas en este documento.
La evaluación pretende mostrar que suponiendo colisiones elásticas de los eterinos con las subpartículas (SPs) que componen la materia ordinaria se produce una fuerza no-nula entre 2 cuerpos materiales A y B que se supondrán (por sencillez en este primer estudio) quietos en el éter.
* Si se hiciera la evaluación en 3D (en 3 dimensiones) se harían las suposiciones siguientes:
- Sean 2 cuerpos A y B formados por materia "ordinaria".
- Para simplificar el cálculo se supondrá que dichos cuerpos son esféricos y que tienen
una distribución de materia (de subpartículas SP) homogénea. También se llamarán A y
B a los puntos centrales de las esferas de materia respectivas.
- Sean rA y rB los radios
respectivos de dichas esferas de materia.
- Sean nA y nB los
números de SPs de que están formados respectivamente los cuerpos materiales A y B.
- Se supone que todas las subpartículas materiales (SP) son del mismo "tamaño"
rS y son "opacas" a los eterinos.
- Se supondrá que para cuerpos A y B de materia "ordinaria" se cumple:
[SG-a] p rA2 >> nA p rS2
p
rB2 >> nB p rS2
lo cual implica que las SP que componen un cuerpo material ordinario apenas se apantallan entre sí. Es decir se supondrá que los cuerpos A y B son altamente (aunque no totalmente) transparentes a los eterinos.
Se puede mostrar (ver otras secciones del Eve Model) que la "masa" (concepto ordinario de la Física convencional) de un cuerpo A formado por materia ordinaria es directamente proporcional al número nA de SPs que lo componen.
* Ahora bien, como se va hacer (al menos de momento y debido a su mayor sencillez) la evaluación en 2D se supondrá en cambio que:
Los 2 cuerpos materiales A y B son planos y de forma circular estando formados cada uno por un número elevado de subpartículas (SP) cuya distribución es homogénea. En este caso las SP serían mini círculos (superficies). También se llamarán A y B a los puntos centrales de los círculos de materia respectivas.
Sean rA y rB los radios respectivos de dichos círculos de materia.
Sean nA y nB los números de SPs de que están formados respectivamente los cuerpos materiales A y B.
Se supone que todas las subpartículas materiales (SP) (opacas a los eterinos) son del mismo "tamaño" rS
Se supondrá que para cuerpos A y B de materia "ordinaria" se cumple:
[SG-b]
rA >> nA rSrB >> nB rS
lo cual implica que las SP que componen un cuerpo material ordinario apenas se apantallan entre sí. Es decir se supondrá que los cuerpos A y B son altamente (aunque no totalmente) transparentes a los eterinos.
Para evaluar la fuerza eterínica sufrida por B se supondrá que el éter que envuelve a los cuerpos A y B puede caracterizarse como sigue:
Supóngase, a efectos de la evaluación, un círculo (dibujado con línea de trazos en la Fig SG-1) en cuyo interior están los cuerpos materiales A y B. Se le llamará a dicho círculo "círculo de evaluación" (CE). Sea por ejemplo r el radio de dicho círculo. Se supondrá (Fig SG-2) que desde cada "punto" P de dicho círculo, o más exactamente desde cada "elemento de arco" de longitud ds de dicho círculo, siendo ds << 2 p r, penetran cada unidad de tiempo hacia el interior del círculo un número grande de eterinos uniformemente distribuidos entre todas las direcciones. Las direcciones que penetran hacia el interior del círculo abarcan un ángulo p (cuya bisectriz sería la dirección que une el punto P en cuestión con el centro del círculo de evaluación).
Se supondrá que por cada arco unidad del círculo CE penetran hacia su interior n eterinos de velocidad v por unidad de ángulo y por unidad de tiempo.
Se supondrá, en un primer cálculo, que todos los eterinos tienen la misma velocidad v (aunque será fácil extender después el cálculo a la suposición de que los eterinos tienen una amplia distribución de velocidades).
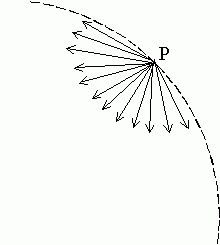
Fig SG-2
NOTA: Como se dijo al principio, se supone que los cuerpos materiales A y B están “quietos en el éter”. Más aún, se asumirá aquí que las subpartículas materiales que componen dichos cuerpos A y B están ellas mismas quietas en el éter. De forma más rigurosa, debe interpretarse que, en el referencial asociado a dichos componentes materiales, la distribución de velocidades de los eterinos del éter es isótropa. Este artículo solo pretende estudiar las implicaciones de las relaciones geométricas que se dan entre los eterinos y las partículas materiales en este caso ideal sencillo de partículas quietas en el éter. (No es el objeto de este estudio analizar la fuerza de frenado del éter sobre partículas materiales que se mueven a través del mismo ni como afectaría dicho movimiento a la fuerza de Le-Sage que se ejercen mutuamente dichas partículas).
La siguiente Figura SG-3 ilustra algunas relaciones geométricas pertinentes para el cálculo.
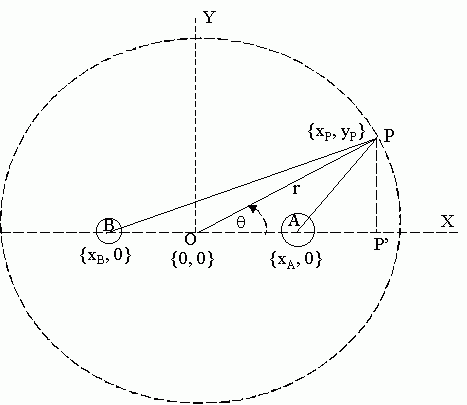
Fig SG-3
El centro O del círculo CE se hace coincidir con el origen {0,0} de coordenadas cartesianas 2D. Los cuerpos A y B se supone que están situados en las posiciones respectivas {xA,0} y {xB,0}.
P’ es el punto proyección de P en el eje de las X.
La distancia PB vale:
[SG-1]
PB = ( P’B2 + P’P2 ) 1/2 = ((xP-xB)2 + yP2) 1/2Supuesto B en reposo, una fuerza eterínica de módulo F portada por eterinos que viajan de P a B tiene las componentes:
[SG-2]
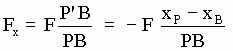
[SG-3]
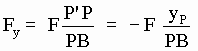
Ahora bien, para integrar después a todos los P (o más exactamente a todos los elementos de arco) del círculo de evaluación, interesa definir la posición de P en función de un parámetro angular. Sea q este parámetro definido como el ángulo que forma el radio vector OP con el semieje +X. En función de este parámetro la distancia PB vale:
[SG-4]
PB = ((r Cos(q)-xB) 2 + r Sin(q)2) 1/2 = (r2 + xB2 -2 r xB Cos(q)) 1/2y las componentes cartesianas de una fuerza eterínica F portada por eterinos que viajan de P a B son (ver [SG-4]):
[SG-5]
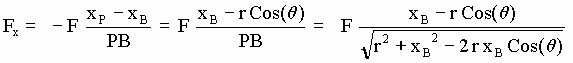
[SG-6]
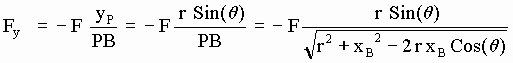
Para evaluar la fuerza sufrida por B debida a la presencia de A se asumirán:
- La probabilidad de que un eterino de velocidad v incidente sobre el círculo B (de radio rB) choque con una de las SP que componen el cuerpo B es PB(v) <<1
- La probabilidad de que un eterino de velocidad v incidente sobre el círculo A (de radio rA) choque con una de las SP que componen A es PA(v) <<1
- Cuando un eterino de velocidad v relativa a un cuerpo material "ordinario" (como A o B) colisiona con una de sus subpartículas, la probabilidad de que sufra una desviación angular (respecto a la dirección inicial de v) comprendida en el intervalo {a, a+da} viene dada por:
[SG-7]
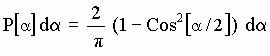
donde la función (1-Cos2[a/2]) es simplemente una hipótesis de trabajo y donde el factor 2/p se ha introducido para normalizar la probabilidad o sea para que:
[SG-8]
Se considera que a la fuerza eterínica sufrida por B contribuyen todos los eterinos que procedentes de cualquier punto del círculo de evaluación CE y sufren alguna de las 3 vicisitudes siguientes:
1) Los que llegan a B sin haberse encontrado con A.
2) Los que llegan a B después de haberse encontrado con A pero habiéndolo atravesado limpiamente A (sin colisionar con ninguna de sus SPs).
3) Los que llegan a B después de haber colisionado con alguna de las SP de A.
Ejemplo del caso (1)
Ejemplo del caso (2)
Ejemplo del caso (3)
Las anteriores figuras son solo ilustrativas pero en la presente evaluación se estudiará el caso (más sencillo de calcular) en el que la distancia AB entre los cuerpos materiales A y B es mucho mayor que cualquiera de dichos cuerpos. Es decir se asumirá que:
[SG-9]
AB >> rAAB >> rB
Se da por sentado (aunque no se pretenderá demostrar de momento) que el cálculo de la fuerza FB sufrida por B no depende del tamaño ni de la posición del círculo de evaluación CE cuyo único requisito es que los cuerpos A y B estén en su interior. No obstante en la evaluación se tomará el centro del círculo CE en un punto de la recta BA debido a lo cual y a la simetría de las colisiones asumida en SG-7, es evidente que la fuerza FB sufrida por B tendrá (por razones de simetría) la dirección de AB siendo nula su componente perpendicular a dicha dirección. Por ejemplo, situando los cuerpos A, B y el CE como en la Fig SG-3 bastará con hallar la componente X de la fuerza FB sufrida por B (siendo nula su componente Y).
---------------------
Antes de pasar a evaluar como contribuyen a la fuerza total FB los tres "grupos" de eterinos descritos arriba se evalúa la fuerza eterínica, que se llamará F0, sufrida por un cuerpo B en ausencia de A y debida por tanto solamente a los eterinos del éter local. Estos eterinos del éter local se suponen representados por esos eterinos de velocidad v que penetran en el círculo de evaluación CE. Imagínese por tanto que B está situado dentro del círculo CE como indica la Fig SG-3 y que A no existe.
Un elemento de arco de longitud ds y de posición P definida por el ángulo q contribuye con una fuerza eterínica sobre B que se puede deducir así:
Tal como se ha dicho arriba, se supone que por cada arco unidad del círculo CE penetran hacia su interior n eterinos de velocidad v por unidad de ángulo y por unidad de tiempo.
A la distancia PB una SP de diámetro 2 rS subtiende desde P un ángulo
[SG-11]
f = 2 rS /PBpor tanto las nB subpartículas de B subtienden en total un ángulo nB .f. Por tanto de los n .ds eterinos que salen del arco ds por unidad de tiempo y por unidad de ángulo, colisionarán por unidad de tiempo con las SP de B n .ds . nB . f eterinos:
Asumiendo, como se postuló en la Sección 1 del "Modelo Eve de Éter", que el impulso eterínico elemental que produce un eterino cuando colisiona con una SP con una velocidad relativa v viene dado por:
[SG-12]
i1 = q v (siendo q una constante numérica)y puesto que la fuerza eterínica se ha definido como el impulso eterínico total por unidad de tiempo, entonces los n.ds.nB.f eterinos de velocidad v antes definidos que impactan con las subpartículas de B por unidad de tiempo contribuyen con una fuerza eterínica:
[SG-14]
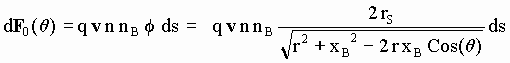
donde se ha expresado la distancia PB de acuerdo con [SG-4].
La componente X de dicha fuerza elemental que es la única de interés (puesto que al integrar después a todo el círculo la componente Y de la fuerza total se anulará por simetría debido a que se ha supuesto que tanto B como el centro del círculo CE están en el eje de las X) valdrá de acuerdo con [SG-5]:
[SG-15]
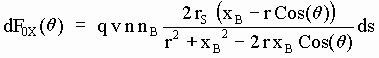
y al integrar a todo el círculo CE, es decir a todos los ángulos q, y puesto que ds = r dq se tiene:
[SG-16]
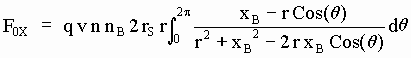
que puede verse que para r > |xB| es
[SG-17]
F0X = 0-------------------------
Se ha mostrado en el cálculo anterior que, supuesto un cuerpo material B en reposo en el éter local, la fuerza eterínica que el éter ejerce sobre B en ausencia de A es cero.
En presencia de A, la contribución conjunta de los eterinos del grupo 1º (los que llegan a B sin haberse encontrado con A) más la contribución de los eterinos del grupo 2º (los eterinos que llegan a B después de haber encontrado A en su camino pero habiéndolo atravesado limpiamente sin chocar con ninguna de sus SP) se puede obtener restando de la fuerza nula calculada anteriormente la fuerza que hubieran producido sobre B los eterinos de aquellos haces PB que en su paso previo por A sufren colisiones con alguna de las subpartículas de este cuerpo A (siendo por tantos retirados del haz de eterinos).
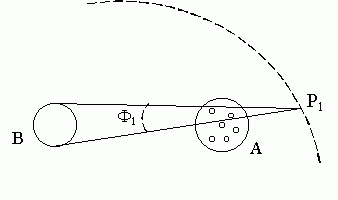
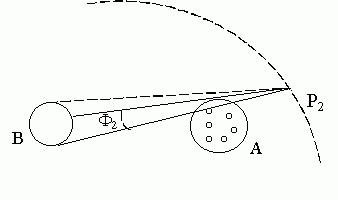
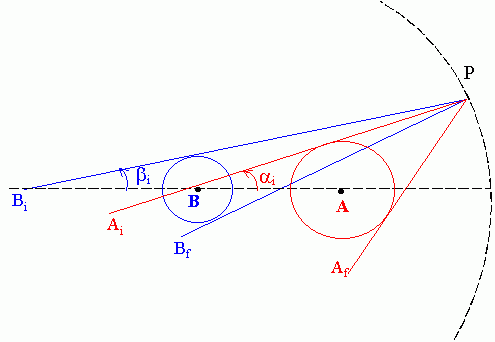
Fig SG-9
Sean
PAi y PAf las 2 semirrectas que pasan por P y son tangentes al cuerpo A
PBi y PBf las 2 semirrectas que pasan por P y son tangentes al cuerpo B
Sean ai, af, bi, bf las direcciones respectivas de esas 4 semirrectas, es decir los ángulos que dichas semirrectas forman con una semidirección de referencia.
Sean a0 y b0 las direcciones de las rectas que unen respectivamente a los puntos centrales de A y B con el punto P.
A efectos de la evaluación, se tomará como "origen" de dichas direcciones 2D al semieje +X, y se adoptará el criterio de que los ángulos que caracterizan a las direcciones (de las rectas pertinentes que parten de P) aumentan en sentido opuesto a las agujas del reloj.
Se tiene (ver la Fig SG-3):
[SG-18]
a0 = XAP = ArcSin[PP’/PA]b
0 = XBP = ArcSin[PP’/PB]
Los ángulos ai, af, bi, bf que forman con el eje X las 4 tangentes a los círculos A y B que pasan por P pueden obtenerse así:
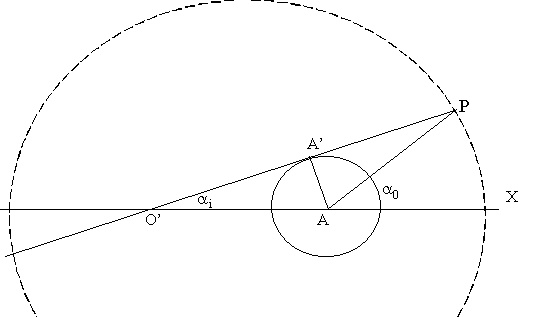 Fig SG-10
Fig SG-10
[SG-19]
ai = a0 – APA’ = a0 – ArcSin[AA’/PA] = a0 – ArcSin[rA/PA]y análogamente se tendrían:
af = a0 + ArcSin[rA/PA]
[SG-19]
bi = b0 - ArcSin[rB/PB]bf = b0 + ArcSin[rB/PB]
En el ejemplo de la Fig SG-9 se ve que los eterinos procedentes de P que se dirigen hacia el cuerpo B (círculo azul) pero pasan previamente por A (círculo rojo) y pueden por tanto sufrir colisiones con alguna de sus subpartículas en vez de llegar a B son los del sector angular AiPBf.
Desde un P genérico, los eterinos procedentes de P que se dirigen a algún punto de B y cuyas direcciones interceptan previamente al cuerpo A están contenidos en el sector angular intersección de los sectores angulares AiPAf y BiPBf
El ángulo abarcado por dicho sector "intersección" viene dado por:
[SG-20]
xAB = Min[af, bf] – Max[ai, bi]Cuando se tome xA> xB como en el presente ejemplo, ocurrirá que cuando xAB es negativo significa que la intersección es vacía (cero).
La siguiente Fig-SG-11 muestra un P desde el cual el ángulo xAB es justamente igual a cero. Para otros P de xP menor dicho ángulo será negativo lo cual implica que desde estos otros P llegan todos los eterinos a B sin haber encontrado a A en su camino. La integración a todo el círculo CE de esta parte de la fuerza eterínica sufrida por B podrá pues restringirse a unos límites qMin y qMax deducibles de la geometría de la Fig-SG-11.
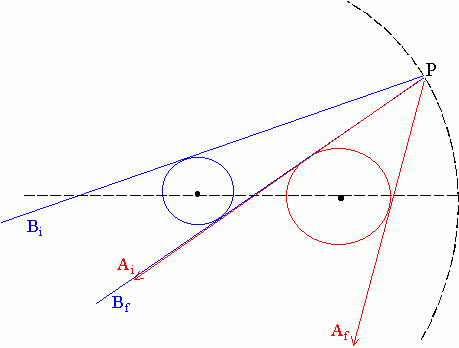
Fig SG-11
El qMax o posición angular de P (representada en la Fig SG-11) a partir del cual la intersección de los sectores angulares AiPAf y BiPBf empieza a ser vacía puede deducirse a partir de la condición (Dirección de PAi) = (Dirección de PBf) es decir:
[SG-22]
ai = bfTeniendo en cuenta [SG-18] y [SG-19] y sustituyendo PP’ = r Sin(q) la condición [SG-22] se traduce en:
a0 - ArcSin[rA/PA] = b0 + ArcSin[rB/PB] =>
[SG-23]
ArcSin[r Sin(q) /PA] - ArcSin[rA/PA] = ArcSin[r Sin(q) /PB] + ArcSin[rB/PB]donde las distancias PA y PB valen:
De forma similar se deduciría el qMin a partir del cual la intersección de los sectores angulares AiPAf y BiPBf deja de ser vacía. En este caso la condición sería:
[SG-22b]
af = bique se traduce en:
[SG-23b]
ArcSin[r Sin(q) /PA] + ArcSin[rA/PA] = ArcSin[r Sin(q) /PB] - ArcSin[rB/PB]aunque teniendo en cuenta que tanto A como B como el centro del CE están situados en el eje X (origen de ángulos q) es evidente por razones de simetría que será qMin = -qMax por lo que una vez deducido el qMax (a partir de la SG-23) no es necesario resolver la SG-23b para deducir el qMin.
No se ha conseguido despejar q en la [SG-23]. No obstante, puede obtenerse una expresión analítica de los q límites (qMin y qMax) en función de r, xA, xB, rA, rB siguiendo este otro cálculo ligeramente más largo.
Desde un punto P del CE el cuerpo A subtiende un ángulo WA = 2 rA/PA
Puesto que A consta de nA subpartículas, en el sector angular xAB definido arriba (ver SG-20) "puede asumirse" que habrá un número de subpartículas dado por nA xAB / WA
Puesto que cada una de estas subpartículas subtiende desde P un ángulo 2rS/PA entonces en conjunto las nA xAB / WA subpartículas subtienden un ángulo:
[SG-24]
(nA xAB / WA) 2 rS/PA = nA xAB PA/(2 rA) 2 rS/PA = nA xAB rS/rAPero de acuerdo con lo supuesto arriba, de cada elemento de arco ds del círculo CE "salen" n .ds eterinos por unidad de tiempo y por unidad de ángulo. Entonces, limitándose a los elementos de arco pertenecientes al arco de extremos qMin y qMax, de esos n .ds eterinos emergentes por unidad de ángulo serán interceptados por las subpartículas de A un número de ellos igual a:
[SG-25]
n ds nA xAB rS/rApor unidad de tiempo. Esos eterinos dejan de llegar al cuerpo B por lo que su fuerza sobre B debe ser restada de la fuerza [SG-17] sufrida por B en ausencia de A que fue calculada arriba resultando ser cero.
Ahora bien la probabilidad de que un eterino incidente sobre el cuerpo bidimensional B (de radio rB) colisione con una de sus nB subpartículas (también bidimensionales pero de radio rS) es :
[SG-26]

donde se ha asumido (ver SG-10) que rB >> nB rS por lo que el cuerpo B es altamente transparente a los eterinos.
Se ha asumido también en [SG-26] que las subpartículas de B están quietas (o tienen velocidades muy pequeñas comparadas con las de los eterinos) por lo que dicha probabilidad PB no depende de la velocidad v de los eterinos.
Entonces de los eterinos que dejan de llegar a B por unidad de tiempo (dados en [SG-25]), habrían colisionado con alguna de sus subpartículas (en caso de no haber sido interceptados por A) los siguientes:
[SG-27]
PB n ds nA xAB rS/rApor unidad de tiempo. Los cuales hubieran producido sobre B una fuerza:
[SG-28]

y de acuerdo con [SG-5] la componente X de dicha fuerza diferencial es:
[SG-29] 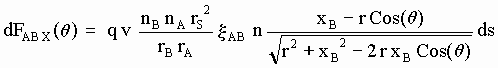
si bien, en el supuesto de que la distancia entre A y B sea mucho mayor que el tamaño de estos cuerpos, para los eterinos pertinentes (procedentes de elementos de arco entre qMin y qMax), será aproximadamente Cos(q) =1 por lo que dichos eterinos viajarían aproximadamente en la semidirección -X y una expresión aproximada más sencilla válida para este caso sería:
[SG-30]
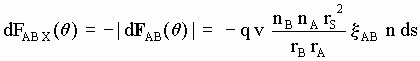
Al integrar a todos los segmentos de arco cuya posición angular q esté comprendida entre qMin y qMax y teniendo en cuenta que ds = r dq :
[SG-31]

donde la magnitud del sector angular xAB (q) dado en [SG-20] puede deducirse a partir de las expresiones [SG-19] y [SG-18].
Nota: La fuerza FAB X dada en [SG-31] es la que producirían, si llegaran a B, unos eterinos ya contabilizados en F0. Pero como no llegan (por ser apantallados por A) la fuerza sufrida por B, a falta de determinar las fuerzas de los eterinos del grupo 3º, será F0 - FAB X = 0 - FAB X = -FAB X
Ya que no se sabe integrar [SG-31] de forma exacta se ha sondeado dicha fuerza mediante integraciones numéricas para distintos conjuntos de valores de r, xA, xB, rA, rB. Se ha observado por ejemplo que la fuerza no depende del valor r del radio del círculo de evaluación elegido. (En concreto la integral de xAB disminuye como 1/r lo cual es compensado por el factor r que aparece delante de la integral).
A continuación se calculará la fuerza sufrida por B debida a eterinos que han sufrido previamente una colisión con alguna subpartícula de A.
Recordando que se viene suponiendo que el círculo CE se mantiene bien alejado de los cuerpos A y B en comparación con los radios rA y rB de estos cuerpos puede entonces suponerse que un punto P de dicho círculo dista aproximadamente PA de cualquiera de las subpartículas que componen el cuerpo A, siendo en rigor PA la distancia entre P y el punto central del cuerpo A. A la distancia PA cada subpartícula subtiende un ángulo 2 rS /PA y en total las nA subpartículas de A (que no se tapan significativamente entre sí) subtienden un ángulo 2 nA rS /PA.
Puesto que del círculo CE "salen" (en cualquier dirección) n eterinos por unidad de arco, por unidad de tiempo y por unidad de ángulo, entonces procedentes del elemento de arco ds centrado en P colisionarán con alguna SP de A los siguientes eterinos por unidad de tiempo:
[SG-34]
2 n ds nA rS /PAPuesto que se ha supuesto PA >> rA todos esos eterinos tendrán la misma semidirección Pà A. A efectos de esta evaluación la semidirección de PA puede identificarse con la de un vector (ver Fig SG-3) con las siguientes coordenadas cartesianas:
[SG-35]
PA = {xA-xP, -yP}Interesan aquí los eterinos que tras chocar con alguna subpartícula de A salen rebotados en la dirección del cuerpo B. Para simplificar el cálculo se supondrá que la distancia AB >> rA y que AB >> rB En este caso desde cualquier subpartícula de A el cuerpo B subtiende aproximadamente el mismo ángulo 2 rB /AB si bien por otra parte puede considerarse a efectos del cálculo que todos los eterino rebotados en A que llegan a algún punto del cuerpo B tienen aproximadamente la misma semidirección que puede representarse por el vector AB de componentes:
[SG-36]
AB = {xB-xA, 0}Ahora bien, de las propiedades del producto escalar de vectores, el ángulo que forma el vector AB con el vector PA viene dado por:
[SG-37]

De acuerdo con la suposición hecha arriba, cuando un eterino de velocidad v relativa a un cuerpo material "ordinario" (como A o B) colisiona con una de sus subpartículas, la probabilidad de que sufra una desviación angular a (respecto a la dirección inicial de v) vale, por unidad de ángulo:
[SG-7b]
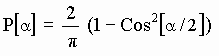
pero la expresión [SG-37] de a = ArcCos(k) invita a aplicar a [SG-7b] la simplificación trigonométrica:
[SG-38] Cos2[ArcCos(k)/2] = 1/2 + k/2y la P[a] dada en [SG-7b] puede sustituirse por:
[SG-7c]
y la probabilidad de que un eterino procedente de P rebote en A hacia algún punto de B vale:
[SG-39]
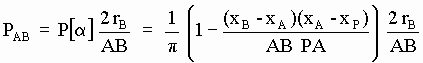
Pero, como se vio arriba en [SG-26], la probabilidad de que un eterino incidente sobre B choque con alguna de sus nB subpartículas es:
[SG-26b]
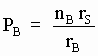
Por lo tanto la probabilidad conjunta de que un eterino tras rebotar en A se dirija hacia B y colisione allí con alguna de sus subpartículas vale:
[SG-40]
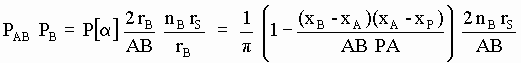
y por tanto (ver SG-34) de los 2 n ds nA rS /PA eterinos que, procedentes del arco ds, chocan con alguna SP de A por unidad de tiempo, los siguientes chocan después, por unidad de tiempo, con alguna SP de B
[SG-41]
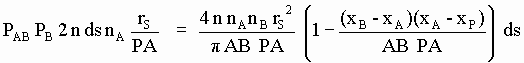
y puesto que un eterino de velocidad v relativa a una SP le comunica un impulso eterínico q v entonces los eterinos pertinentes dados en [SG-41] que (de acuerdo con las suposiciones AB >> rA , AB >> rB ) viajan todos de A a B aproximadamente en la semidirección -X con celeridad v, le producen a B una fuerza eterínica cuya componente X vale:
[SG-42]
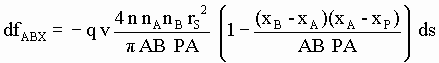
Integrando a todos los elementos de arco del círculo CE y teniendo en cuenta que xP = r Cos(q) y que ds = r dq
[SG-43] 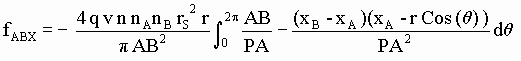
donde AB = |xB-xA|
y donde ![]()
-------------------
Ahora bien, en el cálculo de la fuerza [SG-43] sufrida por B debida a eterinos que han sufrido previamente una colisión con alguna subpartícula de A, se ha supuesto que A es bombardeado desde todas las direcciones por eterinos que provienen del espacio exterior (implementado por el círculo CE) sin que el cuerpo B haya obstaculizado la llegada a A de dichos eterinos. Pero, eso no es cierto para todas las direcciones pues hay un haz de direcciones por las que llegan a A menos eterinos que los que a él se dirigían procedentes del espacio exterior ya que el cuerpo B ha obstaculizado a una pequeña parte de los mismos. La siguiente figura ilustra este caso:

En analogía con el cálculo hecho arriba (ver SG-20) de los sectores angulares que contenían direcciones Pà B que pasan por algún punto de A, ahora, intercambiando los papeles de A y B:
Los eterinos procedentes de P que se dirigen a algún punto de A y cuyas direcciones interceptan previamente al cuerpo B están contenidos en el sector angular intersección de los sectores angulares AiPAf y BiPBf
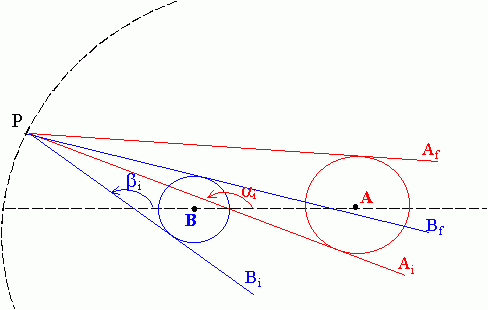
Fig SG-12
El ángulo abarcado por dicho sector "intersección" viene dado nuevamente (al igual que en SG-20) por:
[SG-45]
xBA = Min[af, bf] – Max[ai, bi]Cuando se tome xA> xB como en la Fig SG-12, ocurrirá que cuando xBA es negativo es que la intersección es vacía (cero).

Fig SG-14
Teniendo en cuenta la definición hecha arriba de los ángulos a0 y b0 como los asociados a las direcciones de las rectas que unen respectivamente los puntos centrales de A y B con el punto P:
[SG-46]
a0 = XAP = ArcSin[PP’/PA]b0 = XBP = ArcSin[PP’/PB]
los ángulos ai, af, bi, bf que forman con el eje X las 4 tangentes a los círculos A y B que pasan por P son nuevamente:
ai = a0 - ArcSin[rA/PA]
af = a0 + ArcSin[rA/PA]
[SG-47]
bi = b0 - ArcSin[rB/PB]bf = b0 + ArcSin[rB/PB]
y el ángulo qMin límite de P por debajo del cual el cuerpo B no apantalla todavía al cuerpo A puede deducirse de:
[SG-48]
ai = bf(Nota: a diferencia del cálculo de arriba en el que se analizaba la ocultación de A sobre B, ahora la condición ai = bf permite deducir el q mínimo en vez del q máximo).
Teniendo en cuenta [SG-46] y [SG-47] y sustituyendo PP’ = r Sin(q) la condición [SG-48] se traduce en:
[SG-49]
ArcSin[r Sin(q) /PA] - ArcSin[rA/PA] = ArcSin[r Sin(q) /PB] + ArcSin[rB/PB]De forma similar se deduciría el qMax a partir del cual la intersección de los sectores angulares AiPAf y BiPBf pasa a ser vacía. En este caso la condición sería:
[SG-48b]
af = bique se traduce en:
[SG-49b]
ArcSin[r Sin(q) /PA] + ArcSin[rA/PA] = ArcSin[r Sin(q) /PB] - ArcSin[rB/PB]aunque teniendo en cuenta que tanto A como B como el centro del CE están situados en el eje X (origen de ángulos q) es evidente por razones de simetría que será qMax = -qMin (o si se prefiere qMax = 2p -qMin ) por lo que una vez deducido el qMin (a partir de la SG-49) no es necesario resolver la SG-49b para deducir el qMax .
Nota: El que la misma igualdad [SG-23] o [SG-49] permita deducir los ángulos límites tanto para el apantallamiento de A sobre B como para el apantallamiento de B sobre tiene su explicación en que la ecuación [SG-49] tiene como soluciones cuatro valores distintos de q de los cuales una pareja corresponde al apantallamiento de A por B y la otra al de B por A. Lo mismo puede decirse de la igualdad de las ecuaciones [SG-23b] y [SG-49b].
Desde un punto P del CE el cuerpo B subtiende un ángulo WB = 2 rB/PB Puesto que B consta de nB subpartículas, en el sector angular xBA definido en SG-45 "puede asumirse" que habrá un número de subpartículas dado por nB xBA / WB . Puesto que cada una de estas subpartículas subtiende desde P un ángulo 2rS/PB entonces en conjunto las nB xBA / WB subpartículas subtienden un ángulo:
[SG-50]
(nB xBA / WB) 2 rS/PB = nB xBA PB/(2 rB) 2 rS/PB = nB xBA rS/rBPero de acuerdo con lo supuesto arriba, de cada elemento de arco ds del círculo CE "salen" n .ds eterinos por unidad de tiempo y por unidad de ángulo. Entonces, limitándose a los elementos de arco pertenecientes al arco de extremos qMin y qMax, de esos n .ds eterinos emergentes por unidad de ángulo serán interceptados por las subpartículas de B, antes de llegar a A, un número de ellos igual a:
[SG-51]
n ds nB xBA rS/rBPero la probabilidad de que un eterino incidente sobre A choque con alguna de sus nA subpartículas es:
[SG-52]
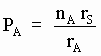
y por tanto el número de colisiones pertinentes (con SPs de A) por unidad de tiempo es:
[SG-53]
PA n ds nB xBA rS/rB = n ds nA nB xBA rS2/(rA rB)De acuerdo con la hipótesis de trabajo hecha arriba, cuando un eterino de velocidad v relativa a un cuerpo material "ordinario" (como A o B) colisiona con una de sus subpartículas, la probabilidad de que sufra una desviación angular a (respecto a la dirección inicial de v) vale, por unidad de ángulo:
[SG-54]
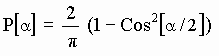
Si, para simplificar, se considera solo el caso en que la distancia AB entre los cuerpos es mucho mayor que el tamaño de estos (o sea AB >> rA y AB >> rB) entonces los eterinos pertinentes, que son ahora los que van de B hacia A y rebotan de nuevo hacia B, viajarían, tanto a la ida Bà A como a la vuelta Aà B, cuasi paralelos al eje X para lo cual deberían sufrir en sus colisiones con las SPs de A una desviación angular a = p .
Por todo ello, de los eterinos contabilizados en [SG-53] (que habrían colisionado con alguna SP de A en caso de no haber sido apantallados por B) habrían llegado de nuevo hacia B los siguientes (por unidad de tiempo):
[SG-55]
P[a] n ds nA nB xBA rS2/(rA rB) = 2/p n ds nA nB xBA rS2/(rA rB)y puesto que la probabilidad de que un eterino incidente sobre B choque con alguna de sus nB subpartículas es:
[SG-56]

estos eterinos (de velocidad v) habrían producido sobre B una fuerza de semidirección –X y de módulo:
[SG-57]
dFBAB = q v PB 2/p n ds nA nB xBA rS2/(rA rB) == q v 2/p n ds nA nB2 xBA rS3/(rA rB2)
Al integrar a todos los segmentos de arco cuya posición angular q esté comprendida entre qMin y qMax y teniendo en cuenta que ds = r dq la componente X de la fuerza en cuestión es pues:
[SG-58]
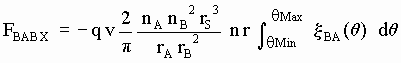
donde la magnitud del sector angular xBA (q) dado en [SG-45] puede deducirse a partir de las expresiones [SG-46] y [SG-47].
Nota: La fuerza FBAB X dada en [SG-58] es la que producirían, si llegaran de vuelta a B, unos eterinos ya contabilizados en la fABX dada en [SG-43]. Pero como no llegan (por haber sido apantallados en su primer paso por el propio B) hay que restar dicha fuerza FBAB X de la fuerza fABX dada en [SG-43].
Se han hecho varias evaluaciones numéricas de las anteriores fuerzas.
Ejemplo 1. Se ha tomado:
q=1 v=1 n=1 nA=1 nB=1 r = 1000 rA=5 rB=3 xA=100 xB= -100obteniéndose:
-
FAB X = 0.020 rS2fABX = - 0.040 rS2
– FBAB X = 0.0042 rS3
Nota: Observese que la fuerza llamada FBAB X incluye un factor adicional rS nB/rB respecto a los parámetros que factorizan las otras 2 fuerzas. Si ocurriese que dicho factor fuese próximo a 1 sería el módulo de FBABX unas 10 veces menor que el de fABX. Ahora bien, puesto que se ha supuesto arriba que rB >> nB rS ello implica que 1 >> nB rS/rB por lo que dicho factor es mucho menro que 1 y el módulo de FBABX será muchos ordenes de magnitud menor que el de fABX y que el de FABX por lo que puede decirse que la fuerza FBABX es despreciable en el escenario asumido en este estudio.
La fuerza total sufrida por B debida a la presencia gravitatoria de A es pues (despreciando FBAB X) en este ejemplo:
FGX = - FAB X + fABX = 0.020 rS2 - 0.040 rS2 = - 0.020 rS2
Se trata por tanto de una fuerza repulsiva puesto que en el ejemplo se han situado A y B de forma que xA > xB
Tras analizar otros ejemplos (y salvo error en los cálculos) puede concluirse que la predicción es que en 2D la fuerza gravitatoria tipo Le Sage es repulsiva.
Ejemplo 2. Tomando:
q=1 v=1 n=1 nA=1 nB=1 r = 2000 rA=1 rB=0.1 xA=200 xB= -100se obtuvo:
-
FAB X = 0.0131 rS2fABX = - 0.0267 rS2
Nuevamente el módulo de fABX es aproximadamente doble que el de FAB X por lo que nuevamente la fuerza total es repulsiva.
Se ha comprobado también con otros ejemplos:
que la fuerza total disminuye con la distancia AB de forma proporcional a 1/AB
que el radio r del círculo de evaluación CE no tiene influencia significativa en el valor de la fuerza total.
Comentarios.
El cálculo en 2D predice que, suponiendo colisiones elásticas entre lo eterinos y las partículas materiales más elementales, la fuerza de Le Sage no es nula. Ello invita a sospechar que en 3D y asumiendo colisiones elásticas la fuerza tampoco será nula en contra de lo que supuso el propio Le Sage (ver por ejemplo http://en.wikipedia.org/wiki/Le_Sage's_theory_of_gravitation ) y vienen repitiendo, sin demostrarlo, varios autores.
No obstante, aunque el apantallamiento eterínico que se producen mutuamente los cuerpos materiales sea responsable de una fuerza entiendo que esa fuerza, llamada de Le Sage, no es adecuada para explicar la gravitación o al menos no lo es por sí sola. Parece por ejemplo difícil de explicar el corrimiento hacia el rojo gravitacional (experimento de Pound & Rebka, etc,...) sin invocar una alteración significativa del espacio en la proximidad de los cuerpos masivos. (Dicha alteración del espacio viene implementada en la Física eterínica por una alteración significativa de la distribución de velocidades de los eterinos). Pero la perturbación eterínica que es capaz de causar el fenómeno de apantallamiento de Le Sage, bajo el supuesto de colisiones elásticas de los eterinos con la materia, no parece ser capaz de predecir un frenado del ritmo de los relojes materiales tanto mayor cuanto mayor sea la masa del cuerpo central y cuanto menor sea la distancia del reloj a dicho cuerpo y a la vez independiente de la masa del reloj.
Por ello pienso actualmente que la gravitación es un efecto residual de los campos electromagnéticos los cuales sí producen una importante perturbación del espacio.
Más aún, si se demostrara matemáticamente que la fuerza de Le Sage es repulsiva, también en 3D, ello invitaría a pensar que dicha fuerza tiene poco que ver con la gravitación y puede en cambio tener mucho que ver con la misteriosa fuerza que parece estar aumentando el régimen de expansión del Universo (asociada a la "energía oscura") descubierta en años recientes.
Sumario de definiciones, constantes y variables:
A cuerpo de materia "ordinaria" que en la evaluación 2D se sustituye por un círculo de materia. También se denomina A al punto central de dicho círculo.
B otro cuerpo circular de materia "ordinaria" aunque opcionalmente de distinto radio y densidad. También se denomina B al punto central del círculo de materia llamado B.
SP Subpartícula elemental de materia de la que están constituidos tanto A como B. También llamada "partícula simple" o Simple Particle. Las SPs son opacas a los eterinos.
rA, rB, rS radios respectivos de A, B y de una SP.
nA, nB
número de SPs que componen respectivamente A y B.Materia ordinaria 2D: se supone que las SPs que constituyen A y B están distribuidas en los mismos de forma homogénea. Se supone asimismo que los cuerpos A y B son altamente transparentes a los eterinos lo cual es consecuencia de asumir:
rA >> nA rS
rB >> nB rS
xA, xB abscisas (coordenadas cartesianas x) respectivas de los puntos centrales de A y B.
AB
distancia entre los cuerpos A y B. En la evaluación es AB = |xA-xB|CE
Círculo de Evaluación. Para implementar una muestra de los eterinos del éter local que baña a los cuerpos materiales se define un círculo virtual de cuyos puntos emerge la misma cantidad de eterinos en todas las direcciones. El CE se define de forma que los cuerpos A y B estén en su interior.r radio del CE.
P
punto genérico del CE.PA, PB
distancias desde P a los centros de respectivamente A y B.O punto central del CE
q ángulo que forma la semidireción OP con la semidirección de referencia +Xn
número de eterinos que emergen del círculo de evaluación CE por cada arco unidad, por unidad de ángulo y por unidad de tiempo.ds elemento de arco del círculo CE
q constante que entra en la definición del impulso elemental que un eterino produce sobre una SP cuando colisiona con ella. (Se definió i1 = q v siendo v la velocidad del eterino relativa a la SP).
v celeridad de lo eterinos pertinentes.
PAi , PAf
semirrectas que pasan por P y son tangentes al círculo que define al cuerpo APBi , PBf
semirrectas que pasan por P y son tangentes al círculo que define al cuerpo Bx
AB sector angular intersección de los sectores angulares subtendidos desde P por los cuerpos A y B. Mide el apantallamiento que desde el punto de vista de P produce el cuerpo A sobre el cuerpo B.x
BA igual que xAB pero aplicado a la evaluación del apantallamiento que desde el punto de vista de P produce el cuerpo B sobre el cuerpo A.a
i, af ángulos que forman con el eje +X las 2 tangentes trazadas desde el punto P al círculo que representa al cuerpo A. bi, bf ángulos que forman con el eje +X las 2 tangentes trazadas desde el punto P al círculo que representa al cuerpo B.a
0, b0 ángulos que forman con el eje +X las rectas que unen respectivamente a los puntos centrales de A y B con el punto de evaluación P.