Feb 2005
Periodic disturbance observed at a detector produced by a non coherent monochromatic distant emission.
A generic emitter of radiation can be considered to be some matter with an inner structure that oscillates in time with a frequency n. The matter redistributes the aetherinos of the environment aether that collide with it. When the oscillation passes a "maximum" it can be considered that from the emitter emerges in some direction an excess of aetherinos (respect to the number that emerge in absence of the oscillation). When the oscillation passes a "minimum" it can be considered that along that direction emerges a deficit of aetherinos. The requisite (described in Section 6) that the effective speed of the disturbance must have a constant value relative to the detector (independently of the speed of the detector relative to the emitter) can be fulfilled if such excess (or deficit) is distributed along the aetherino speeds relative to the source as follows:
[6A-1]
where r(v) dv is the excess/deficit in the number of aetherinos of speed {v, v+dv} that emerge along the given direction. Therefore for example in the case of an harmonic oscillatory emitter, the number of aetherinos that emerge along a given direction during the time interval {t, t+dt} could be represented by:
[6A-2] 
Note: The speed distribution [6A-1] and model of emission [6A-2] are only simplifications of what is considered a more generic model of emission (based on an oscillating redistribution of aetherino speeds such that at any given epoch the emitter produces simultaneously an excess of low speed aetherinos together with a deficit of the fast ones, or vice versa). A detailed description of this generic model of emission (and a simulation based on it) will be presented when possible.
An aetherinical wave consistent with the concept of aetherino adopted in this work would have the following features:
In a "standard" gas, pressure waves dissipate quickly, but the proposed model
of aether is made of quasi-classical "particles" (aetherinos) that do not
collide with themselves and therefore this aether behaves very differently from a standard
gas. The aetherinos do not interact between themselves because it is assumed that (1)
their "size" is so small that their probability to collide (touch) is negligible
(but not because their volume density is small), and (2) because it is assumed that there
is by definition no force acting "at a distance" between aetherinos because the
aetherinos are themselves the vehicles of all known physical forces.
In another section of this work it was also said:
'... The molecules of a standard gas interact with each other making the gas tend towards homogeneity and equilibrium. The pressure waves that the gas can carry soon dissipate. On the contrary the aether proposed cannot carry pressure waves because the aetherinos do not "push" each other, but, if by some mechanism a group of aetherinos is endowed with a given velocity v these aetherinos will travel "unlimited" distances maintaining their initial velocity and consequently their initial spatial distribution (i.e. their relative positions making some kind of moving packet) until they find matter with which collide. Similarly, if the emitting mechanism produces a default of aetherinos of a given velocity (respect to the mean density of aetherinos of that velocity),this "default" will travel through vacuum maintaining its structure until it encounters matter. Of course, the word "unlimited" is used in a restricted sense since the chance of having a group of aetherinos endowed with "the same" velocity tends to zero as the velocity is singled out with more precision. In consequence a dissipation of the initial spatial structure must take place.'
Note: the interesting feature of the aether-wave dissipation just mentioned, is actually a gradual longitudinal enlargement (spread) of the disturbance (in addition to the standard 1/d2 angular spread). To visualize what is meant by the "longitudinal spread of the disturbance" it might be helpful to abstract those aetherinos emerged from the emitter during a small time interval
Dt with a given direction and with speeds in a small interval {c-Dv,c+Dv} centered on c. That group of aetherinos can be considered to implement a "wavepacket". It is evident that the spatial "width" of this group of aetherinos along their direction of advance increases with time (or equivalently with their distance to the emitter).Expected consequences of the longitudinal spread of these aetherino-implemented waves are the following:
(a) the longitudinal spread implies that disturbances emitted later will gradually mix with disturbances emitted earlier at a smaller speed (i.e. successive "wavepackets" of different speeds will gradually overlap).
(b) in the case of a long lasting emission of constant frequency, it is expected that the longitudinal spread should not affect the integrity nor the power of the carrier wave even in the case of non coherent emission. It is well known that adding waves of equal frequency but random phases produces a wave of the same frequency but whose intensity is the sum of the intensities of the components. Therefore this flying apart of aetherinos emitted at the same epoch, should not destroy the frequency feature of the basic carrier wave that is constantly rebuild with the faster aetherinos catching up from behind (emitted later at the source) and by the slower aetherinos being caught up (emitted earlier).
(c) if the constant-frequency carrier wave is modulated (as for example in the case of intensity or frequency modulated radio broadcast waves) it is instead expected that the longitudinal spread of the aetherinos will gradually degrade the modulation.
- In the case of a fully coherent harmonic emission as for example the one given above:
[6A-2]
an analytical expression of the detected disturbance can in principle be sought. It is just a matter of adding all the aetherinical impulses suffered by the detector at a generic epoch T (e.g. integrating for all the aetherino speeds and having in mind that the aetherinos of speed v reaching the detector at the epoch T have emerged the detector at an epoch t = T-d/v where the number of emerging aetherinos was given by 6A-2). (The results of this calculus are under revision and will be presented as soon as possible).
- In the case of a non coherent emission of "monochromatic" radiation of basic/average frequency n, it is not so evident that the longitudinal spread and space mixing of the aetherinos will not finish by destroying all traces of the basic emitted frequency n when the disturbance is observed at sufficiently far detectors. It now seems impossible to obtain an analytical expression for the superposition of random-phased wave-trains and therefore a computer simulation has been made to deduce the predictions of the model. The details of how has been implemented the simulation are given below. The result of this (preliminary) simulation is that the detector does detect a periodic disturbance of frequency n.
Simulation.
(The following assumptions about coherence does not pretend to be a rigorous description of these phenomena that are successfully and rigorously described by mainstream Optics using a very specific terminology. At this somewhat qualitative state of the aether model it would add unnecessary complications to the "generic description" of the aetherino waves and of the simulation, that are what is pretended here).
A typical monochromatic non-coherent source of light can be conceived as the superposition of a big number of elementary monochromatic wave trains of finite length emitted at random times from different points of a material body. Each elementary wave train can be imagined to be a succession of a big (but finite) number of equally spaced wave fronts. (In a monochromatic light, all the wave trains are supposed to have that same spacing l between their wave fronts). The "source" of radiation to be used in the simulation will be supposed to be the net disturbance produced in some small window W of the emitter as the result of the superposition of the plurality of wave trains continually reaching such point. Depending on the average rate of new trains reaching W and on the average number of l-spaced wave fronts of each train, a different degree of coherence will be obtained in the resultant wave. Each time a new wave train adds to the previous superposition of wave trains the resultant wave will suffer a "small" phase shift. Similarly each time an old wave train finishes its pass by W it stops to contribute to the superposition and the resultant wave will suffer another "small" phase shift. (The "smallness" of those constantly happening phase shifts will depend, as said before, on the average rate of new trains reaching W and on the average number of l-spaced wave fronts of each train). The resultant disturbance (of ever-changing phase) can be modeled by a succession of wave fronts leaving W, no longer with a perfect periodicity 1/n (like would be the case for a perfectly coherent wave), but at random time intervals each very close to 1/n and whose average is 1/n.
This "non-coherence" has been implemented in the simulation like this:
t(i) = t(i-1) + 1/n + (1/n) (1-K) Random(-1,1) [6A-3]
t(i) is the epoch of departure of the ith wave front.
n
is the nominal (and average) frequency of the emitted disturbance.Random(-1,1) is, for each i, a fresh random real number between –1 and 1
K is a constant (between 0 and 1) that somehow defines the "coherence" of the emission.
Let d be the distance between the emitter W and the detector. (It is supposed in this simulation that the detector is at rest relative to the emitter).
The signal received by the detector has been calculated for 24 contiguous time intervals each of which has a duration of 1/8 of the average period of the wave (1/n) . For example supposing that the observation starts at the epoch T0 , the following detection intervals are simulated:
{T0, T0+3/(24n)}, {T0+3/(24n), T0+2*3/(24n)}, …, {T0+23*3/(24n), T0+24*3/(24n)}
Therefore the simulation and the graphics below span a time interval of 3 average wave periods and contain a total of 24 disturbance evaluations.
To compute the disturbance received by the detector during one of its observation intervals, e.g. between T0 +(i-1)/24n and T0+i/24n, the following suppositions have been made:
(1) every emitted wavefront is made of a big number of aetherinos of a plurality of speeds directed towards the detector. As soon as a wavefront leaves the emitter it divides itself therefore in a continuum of subfronts of different speeds.
(2) a subfront of speed v (or more precisely, made of aetherinos with speeds in {v, v+dv}) contains by hypothesis
v2 Exp[- 2v/V]dv aetherinos. (The uppercase V is a constant. It actually is the speed for which such distribution reaches its maximum).
(Incidentally it is shown in Section 6 that a distribution of the type v2 Exp[- 2v/V]dv makes the disturbance have a constant speed c=2.5 V relative to the detector independently of the speed of the detector relative to the emitter. More generally, any emission for which the disturbance has an aetherinical distribution of the more general type vn Exp[- k.v/V] dv (or a linear combination of these types of functions) does also make the disturbance have a constant speed relative to the detector).
(3) an aetherino of speed v relative to the detector contributes with an impulse (or disturbance) proportional to v. Therefore a subfront of speed v contributes with an impulse proportional to v3 Exp[- 2v/V]dv when it reaches the detector.
(4) In the simulation, instead of supposing an emission whose strength varies continuously between 2 wavefronts as Cos(2pnt), it has simply been supposed that a time 1/(2n) after each emitted wavefront is emitted a "wave-through" (or "deficit" of aetherinos in relation with the average number of aetherinos in the aether) with the same, but negative, speed distribution. Therefore each "sub-through" of speed v (i.e. deficit of aetherinos propagating at speed v) contributes with a negative impulse -v3 Exp[- 2v/V]dv when it reaches the detector.
(5) A computer simulation can of course not account for the contributions of all the aetherinos because their speeds span an infinite interval {0, Infinite}. Cuts have then been introduced in the sampling of speeds. Only the contributions of aetherinos with speed v in {V*a, V*b} have been sampled (a and b are numerical constants and the simulation has been tested using for them different values). For example:
- Supposing that the simulation makes 24 observations starting at T=0 and ending at T=3/n (i.e. the observation intervals are {0,3/(24n)}, {3/(24n), 2*3/(24n)}, {2*3/(24n), 3*3/(24n)}, …, {23*3/(24n), 24*3/(24n)} ) then if the slowest aetherino speed taken into consideration is V*a , the first emitted wavefront to be accounted for in the simulation (that corresponds to T=0 in the first interval of observation) must have been emitted at approximately t 1 = T-d/(V*a) = -d/(V*a). And the last emitted wavefront to be accounted for in the simulation (that corresponds to T=3/n in the first interval of observation) must have been emitted at approximately t n = 3/n-d/(V*b). On the whole considering that there is on the average one emitted wavefront every 1/n seconds, to perform the simulation one must previously obtain (using [6A-3]) the emission epochs of at least
n = ( t n - t 1)*n = (3/n -d/(V*b) + d/(V*a)) *n wavefronts.
for example taking a = 0.12, b = 6, n = 1, V = 0.4, d = 106 => n = 2.04*107 wavefronts
(Note: the reason for taking the speed V, for which the distribution v2 Exp[- 2v/V] reaches its maximum, equal to 0.4 is because in Section 6 it was found that waves based on such distribution have an effective (signal or modulation) speed c=2.5*V giving in this case c=1. Since c=1 and n=1 imply a nominal wavelength l=1 that means that, even working with such high number 2.04*107 of wavefronts, the simulation is only considering observation distances between emitter and detector of 106l. But the results of the simulation show that the amplitude of the periodic disturbance observed at the detector does not decrease with the distance d (except for the trivial 1/d2 solid angular spread in 3-D).
The simulation does the following:
(a) makes a list of the emission epochs of approximately 2.2*107 wavefronts using the expression [6A-3] mentioned above
t(i) = t(i-1) + 1/n + (1/n) (1-K) Random(-1,1)
(b) for each of the 24 detection intervals, e.g. for the ith {T0+(i-1)*3/(24n), T0+i*3/(24n)} :
(b1) for each of the 2.2*107 wavefronts, e.g. for the jth emitted at t(j) it is first found if such wavefront must add to the disturbance being evaluated:
the aetherinos emitted at t(j) and reaching the detector at the end of the pertinent interval of detection have a speed vSLOW = d/( T0+i*3/(24n) - t(j) )
the aetherinos emitted at t(j) and reaching the detector at the beginning of the pertinent interval of detection have a speed vFAST = d/( T0+(i-1)*3/(24n) - t(j) )
if both speeds are within the limiting aetherino speeds that have been defined to contribute, i.e.
if vSLOW > a*V and vFAST < b*V then the following contribution is added to the disturbance of the pertinent detection interval: v3 Exp[- 2v/V] taking v = d / (T0+(i-1)*3/(24n) + (1/2) 3/(24n)- t(j) ) i.e. assuming an average v equal to the one that would have an aetherino departing the emitter at t(j) and reaching the detector at the central epoch of the ith detecting interval.
it is similarly found if the wavethrough emitted just after this jth wavefront must add to the disturbance being evaluated: That wavethrough was emitted at th(j) = t(j) + [t(j+1) - t(j)]/2
the deficit of aetherinos emitted at th(j) and reaching the detector at the end of the pertinent interval of detection have a speed vhSLOW = d/( T0+i*3/(24n) - th(j) )
the aetherinos emitted at t(j) and reaching the detector at the beginning of the pertinent interval of detection have a speed vhFAST = d/( T0+(i-1)*3/(24n) - th(j) )
if both speeds are within the limiting aetherino speeds that have been defined to contribute, i.e.
if vhSLOW > a*V and vhFAST < b*V then the following contribution is added to the disturbance of the pertinent detection interval: -vh3 Exp[- 2vh/V] where vh = d / (T0+(i-1)*3/(24n) + (1/2) 3/(24n)- th(j) )
(c) Finally the 24 outputs are printed in the debug window of the VisualBasic6 interpreter in an adequate format to be easily copied and pasted into a Mathematica ListPlot:
Debug.Print "{"; T0+(i-1)*3/(24n) +0.5* 3/(24n); ","; Format(disturbance(i), "0.##########"); "},";
All the graphics below correspond to a distribution with V = 0.4 and to an emitted frequency
n=1.All the graphics below correspond to (1-K) = 0.02 , except Fig[6A-11] for which a smaller "coherence" has been tried taking (1-K) = 0.2
All the graphics below represent the "disturbance" (or aetherinical impulse) received by the detector as a function of time T. As said above the observation time (horizontal axis) spans a time interval equal to 3/
n (i.e. equal to three times the period of the emitted wave). To evaluate the detected "disturbance" it has been assumed that an aetherino produces an impulse (or momentum increase) proportional to the velocity v of the aetherino relative to the detector. Similarly a "deficit" aetherino of velocity v (in respect to the average number of aetherinos of velocity v in an "undisturbed" aether) is assumed to produce on the detector an impulse proportional to –v.d = distance between emitter and detector
Only the contribution of those aetherinos of speeds v such that (a V) < v < (b V) has been added to the disturbance. (V is the speed for which the emitted wavefronts have a maximum number of aetherinos).
[6A-5]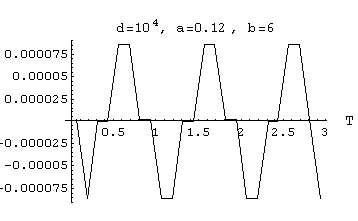 
output Amplitude = 0.86 *10-4
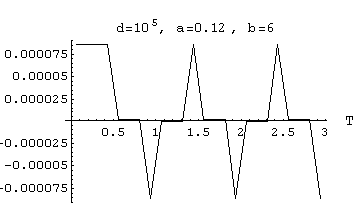output Amplitude =
0.85 *10-4
[6A-7]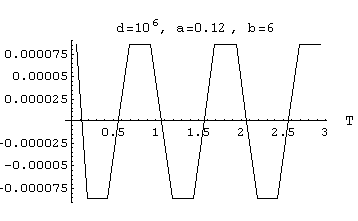 
output Amplitude = 0.85 *10-4
[6A-8]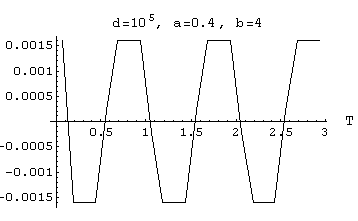 
output Amplitude = 1.6 *10-3
[6A-9]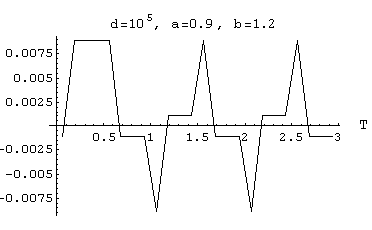 
output Amplitude =
0.9 *10-2
[6A-10]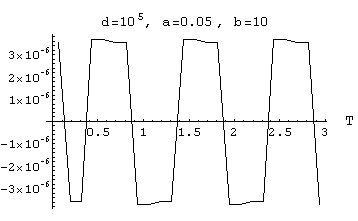 
output Amplitude = 3.55 *10-6
[6A-11]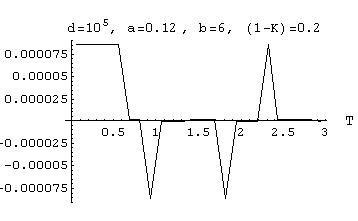 
output Amplitude =
0.85 *10-4