Fig[5-1]Warning
This paper became obsolete in 2011 when the model
adopted the paradigm of "two types of aetherinos" (p and n) and
started describing the redistributions of aetherinos by matter assuming a
"type switch" of the aetherinos when they collided with matter of the
opposite type.
(In this old paper only one type of aetherinos was
assumed. The redistribution of aetherino speeds depended on the type of matter
with which they collided. The two types of matter assumed before 2011 had
resonances to aetherino collisions at different relative speeds and changed the
speeds of the colliding aetherinos in different amounts).
Furthermore at the epoch in which this paper was
written (about the year 2002) the model assumed that, due to the aether drag,
all the particles of the universe decreased their speeds in an asymptotic way,
according to the same law, when observed by the Ideal Observer (IO) (Note: for
the Ideal Observer all the aetherinos travel at constant velocity until they
collide with matter). Such speed decrease included a slowdown of the orbital
speeds of electrons in atoms, planets around stars, etc..
But lately the model assumes that the aether drag does
not slowdown the orbiting bodies bound by forces of attraction, mainly because
of "the forward force".
The paper has not been removed because it is considered
that it contains paradigms that could be of interest in other domains of
Physics.
5 - Force on a moving body.
Abstract: - A calculus is made of the aetherinical force suffered by a body B that moves relative to a body A that is responsible of the material force. (A is a subject of forces due to the redistribution of velocities in the aetherinos that collide with it). It is found that, even for a significantly big velocity u of the target body B relative to the source body A, the force detected by B at the epoch t is directed approximately along the direction AB at this same epoch t. (This fact, although "explained" by the Theory of Relativity, was a problematic feature called "action at a distance" of Newtonian Physics). For example, calling c the average speed (relative to A) of the aetherinos carrying the force, it is found in the calculus made below that if at the epoch t the target body B moves relative to A with the quite big speed 0.1c in a direction perpendicular to AB it experiences a force whose direction differs from AB by approximately 0.05o This is a rather small angle considering that most classic models would predict that, if the disturbance producing the force is carried at speed c relative to A, the body B should feel the force of A with an aberration angle of ArcTan[0.1c/c] = 5.71o It is also found that the modulus of the force suffered by B due to the influence of the material body A decreases when the speed of B relative to A increases. This dependence on the relative velocity is a general feature of the material forces studied in this work that are due to the redistribution of aetherino velocities originated at some piece of matter. Reasoning (as in Annex D) that the strength of the force caused by A increases if the internal component Simple particles making A have a faster speed (therefore producing a sharper redistribution of aetherinos) it can be predicted that the force experienced by a body B placed at a very large distance from A decreases less than their inverse squared distance. This is due to the fact that very big distances imply very big time intervals between the average epoch at which the force carrier aetherinos depart A and the epoch at which their influence is measured at B. But, at an epoch much earlier than the one at which the force is being measured at B, all material composite bodies (like for instance A) had faster internal speeds because, in general, all material particles are decreasing their speed in time due to the aether drag force. This prediction suggests the possibility to explain the anomalous rotation curves of galaxies without invoking the existence of dark matter. |
Fig[5-1]
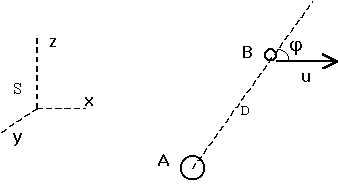
Let S be the reference frame of description. Let the aether be at rest in S. Let a material body A be at rest in S and let a material body B move in S (and hence relative to the aether) with velocity u along the X axis of S. The force that A exerts on B at the epoch t will be analyzed. Let D be the distance between A and B at this epoch t. Let the straight line AB be parallel to the XZ plane (i.e. AB together with u constitute a plane parallel to XZ). Let j be the angle that the semidirection AB makes with the velocity u (and hence with the axis X) at the epoch t of description. Let the "size" of the interacting bodies A and B be much smaller than D.
The body B is subject to the following two forces:
FD = Aether drag force = aetherinical force that B would suffer in the absence of A (but otherwise in the same environment) due to the unbalanced impulses of the aetherinos from the surrounding aether reaching it from all directions. Since u is the velocity of B in the aether rest frame, this drag force acts in the direction of - u. As explained in other sections of this work the aether drag force does not contribute to the movement observed by the Official Observer OO (i.e. by us that use official real clocks) and can therefore be ignored in this context.
F
M = Material force exerted by A = aetherinical force due to the aetherino's velocities redistribution originated at A. This redistribution has been described (see Section 1 and Annex D) by a "residual" distribution which is obtained by subtracting the scattered distribution sA(v) from the emergent distribution nA(v). The scattered distribution sA(v) is the distribution of velocities, before their collisions with A, of the aetherinos that collide in unit time with any of the Simple particles forming A. The emergent distribution nA(v) is made by the distribution of velocities, after their collisions, of the aetherinos that collide in unit time with any of the Simple particles forming A.The total aetherinical force acting on B can then be written:
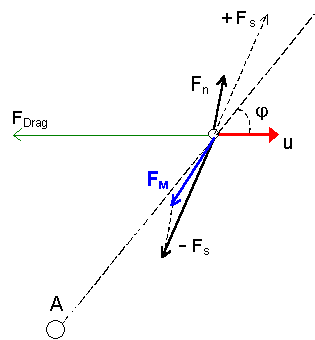Fig [5-2]
Imagine by the moment that B has no internal moving component particles (e.g. B is a Simple Particle). This restriction together with the requirement that A and B are small compared with D can later be removed considering that the aetherinical forces behave as vectors and the total force that a "big" body A exerts on B is just the vector sum of the forces exerted by all the "small" parts in which A can be considered divided for description purposes. In a similar way the results can later be generalized to the case where B is big and composite, adding the forces suffered by all its small component particles.
(Repeating once more the reasoning of preceding sections) the material aetherinical force F
M that A exerts on B can be calculated as follows:- Consider first the force Fn due to the emergent aetherinos of A.
In the vicinity of B, the density of aetherinos with speeds in {v, v+dv} that have emerged from A is:
[5-3]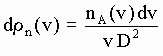
where:
drn(v) is the number of such speed {v, v+dv} aetherinos in unit volume at the position of B.
nA(v) is the number of speed v aetherinos emerging from A by unit time, by unit speed interval and by unit solid angle after having collided with any of the internal Simple particles making A.
In the reference frame S chosen for the description (associated with A) the velocity direction of all the aetherinos that, having emerged from A, collide with B at the epoch t is equal to the direction AB of the vector joining A and B at the epoch t.
Note: The expression [5-3] should be evident considering that, according to the definition of nA(v)dv as a flux by unit solid angle, nA(v)dv/D2 is the number of aetherinos (of speeds in {v, v+dv}) crossing in unit time, at the vicinity of B, a unit area surface placed perpendicular to AB. The number of aetherinos of speed (approximately) v having crossed such unit surface in a unit time interval can therefore be found in an imaginary "quasi-cylinder" of unit base and length v whose volume has therefore a magnitude equal to that of the speed v.
When an aetherino proceeding along the semi direction AB collides with B it gives to this body an impulse q vR (where vR = v - u is the velocity of the aetherino relative to B). Therefore for an aetherino of speed v in S, the Cartesian components of this elementary aetherinical impulse are (see Fig[5-1]):
iX = q.(v - u)X = q.(v Cos j - u)
[5-4] iY = q.(v - u)Y = 0
iZ = q.(v - u)Z = q v Sin j
The number of collisions in unit time between B and the pertinent aetherinos (those whose density is given in [5-3]) can again be calculated considering that in the special reference frame where these pertinent aetherinos (of speed v) are at rest the body B of geometric cross section s sweeps in unit time a cylindrical volume of length vR. Hence this rate of collisions is:
[5-5] 
The aetherinical impulse given to B by all these collisions occurring in unit time has therefore the components:
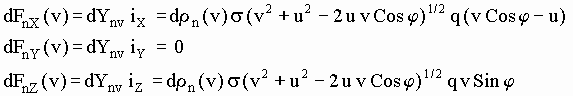
The components of the aetherinical force Fn are finally obtained adding for the pertinent aetherinos of all speeds:
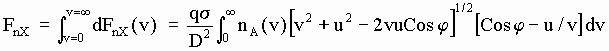
[5-7] 
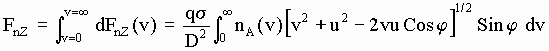
With a similar calculus, the aetherinical force Fs that the aetherinos scattered by A would produce at B if they had not been scattered, has the components:
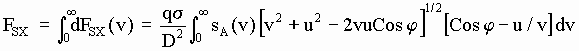
[5-8] 
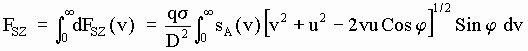
obtained by simple substitution of nA(v) by sA(v) in [5-7].
These aetherinical forces Fn and +Fs have been represented in Fig[5-2]. Notice that for u>0 neither Fn nor +Fs act along the direction AB. The reason is that the impulse produced by a colliding aetherino acts along the direction of the velocity of the aetherino relative to the target B. (The aetherinical force is just the vector sum of the pertinent elementary impulses produced in unit time).
For a given u, the smaller the speed v (in frame S) of the colliding aetherinos the bigger the deviation from the direction AB of their velocity relative to B. In Fig[5-2] Fn has been drawn weaker and more deviated from AB than + Fs . This example would correspond to a body A redistributing the aetherinos in such a way that the aetherinos "scattered" at A had on the average faster speeds v than the aetherinos "emergent" from A (after their redistributing collisions). Recalling that the material force is FM = Fn - Fs , the "A-scattered" part of the force acting on B is not + Fs but its opposite - Fs . This example of Fig[5-2] represents therefore an attraction of B by A.
NOTE 5-1
The value of the material force FM = Fn - Fs acting on B could be argued to correspond to the force in the reference frame associated to the moving target B since it depends on the values of the aetherino impulses that on its turn depend on aetherino velocities relative to B. But actually the aetherinical forces of this model are Galileo invariant between all "inertial" (or more exactly "rectilinear") referential frames because the increments of velocity that the aetherino collisions give to the particles, and hence the aetherinical impulses, are Galileo invariant. (Remember that an "aetherinical force" is defined as the net aetherinical impulse by unit time and that it is also a postulate of this model, see Section 3, that an aetherinical impulse produces a given velocity increment. But a velocity "change" does not depend on the velocity of the reference frame from which it is observed since the Galilean reference systems use the same clocks and the same space standards). The speeds and velocity directions of the colliding aetherinos do of course depend on the reference frame but not the velocity changes given to the particles and hence the impulses. Neither the direction nor the modulus assigned to an aetherinical force depend on the velocity of the reference frame chosen for the description of the force. The values of the forces calculated above (i.e. their moduli and directions) are therefore also the values to be used in the dynamics of the reference frame S of description (associated in this example to A). Therefore, if a universal law of the type F=m.a is to be considered valid in all inertial reference frames, and since both the force F and the acceleration a are Galileo invariant, it follows that the mass m of the body suffering the force should not depend on the frame of description. The relativistic mass increase (observed in many experiments) can only be accounted by this aether model as an effect due to the absolute speed of the mass relative to the aether and not due to its speed relative to the description frame. It seems plausible that the speed of the Earth relative to the aether is much smaller than the speeds at which the "mass increase" effect begins to be measurable in our labs and that explains why mainstream Physics has not yet realized that such apparent mass increase is due to the absolute speed and not to the lab speed of the high energy particles.
It has also been supposed that the influence on B of the aetherinos scattered by A is given by a force - Fs (equal and opposite to Fs). It seems easy to understand how a colliding aetherino acts on B but it is not so evident to understand the influence on B of the missing aetherinos scattered at A. To understand the effect of the missing (or deficit) aetherinos it must be remembered that from the point of view of the official observer, a standard non disturbed aether exerts no net force on material bodies. But if some aetherinos are removed from such aether the net force of the remaining aetherinos does no longer cancel. In Section 7 it is defended that, within the aether sea of aetherinos acting on B, the effect of a missing aetherino (not) colliding with B must be accounted for by the impulse of an aetherino whose velocity relative to the target B is opposite to the relative velocity attributed to the missing one. (The reason is based in the following: suppose that the missing aetherino has velocity v in frame S and velocity vR relative to B. It can be imagined that the body B at a given instant does not suffer any force if it is receiving the simultaneous collisions of an aetherino of relative velocity vR and another of relative velocity - vR. On the contrary it would be incorrect to equate the effect of a missing aetherino of velocity v in S with that of an aetherino of velocity -v in S because an aetherino of velocity -v relative to S does not have in general a velocity - vR relative to B and is therefore unable to cancel the force produced by a simultaneous collision of the aetherino of velocity v relative to S).
---------------------------
Two types of transformations are used in this work that should not be confused:
- Transformations between moving reference frames for one given type of observer (either Ideal or Official) that are related by the Galileo transformation. (The frames related use the same clocks and the same space standards).
- Transformations between the two different types of observer (Ideal and Official) that use different type of clocks.
A confusion must also be avoided between the two uses of the word "force" made in this work:
- Aetherinical force: defined basic concept depending on the values of the velocities assigned by IO to the colliding aetherinos.
- Official force or simply force: the familiar (in standard physics) magnitude equal to the linear momentum increase in unit time, that is described by the model as the OO value of the corresponding IO (aetherinical) force.
---------------------------
The total aetherinical force F (including the aether drag force) acting on B at time t will in general have a direction that differs greatly from the central direction AB. But, as shown below, the aetherinical material force FM = Fn - Fs (excluding the drag) will have, as long as the speed u of B relative to A is not big compared with the average speed of the aetherinos, a direction very close to that of AB at the same epoch. The direction AB has been characterized in Figs[5-1] and [5-2] by the angle j. Calling p the following adimensional quantity:
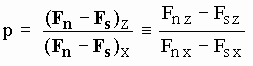[5-9]
then the direction of the aetherinical material force FM suffered by B can be characterized by ArcTan[p]. But from [5-7] and [5-8]:
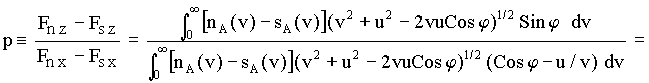
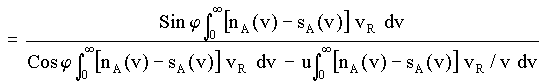[5-10]
where v
R = (v2 + u2 - 2 u v Cos j) 1/2 is the speed relative to B of an aetherino traveling from A to B with a speed v in S. The behavior of [5-10] has been computed for several values of u and j using as nA(v)-sA(v) the example residual distribution Eq[D-11] presented in Annex D. (Notice that the u appearing in Eq[d-11] has been called v in this Section).Summarizing the results of this computation, Table[5-10] gives the angle j - ArcTan[p] in degrees for different angles j (columns of the Table) and for three values of the speed u of B (rows of the Table). Notice that j - ArcTan[p] is the angle between the direction AB at the epoch t and the direction of the material force suffered by B at this epoch t :
| 18º | 36º | 54º | 72º | 90º | 108º | 126º | 144º | 162º | |
u=VM/10 |
-0.11 | -0.18 | -0.16 | -0.07 | 0.05 | 0.16 | 0.21 | 0.20 | 0.12 |
| u=VM/3 | -1.19 | -1.50 | -0.88 | +0.30 | 1.57 | 2.53 | 2.88 | 2.50 | 1.45 |
| u=VM | 1.10 | 7.62 | 15.7 | 23.8 | 31.2 | 37.6 | 42.1 | 42.5 | 32.7 |
VM is the speed for which the aether canonical distribution reaches its maximum. (This canonical distribution plays a role in the calculus of the redistribution n(v)-s(v) as for example in Eq[d-11]. To evaluate the example material force produced by A, the internal speed w of the SPs forming A has been taken w=0.1VM To obtain an attraction force the constant g of Eq[d-0b] and Eq[d-11] has been taken g=0.05).
It seems interesting to note that, for not too big speeds u of the body B, the direction of the material force exerted by A acts in a direction very close to that of AB at the same epoch. This reminds the standard interpretation of the "action at distance" forces of Newtonian physics, i.e. the intrinsic supposition of Newtonian physics that the gravitational force of planet A on planet B propagates at infinite speed. Here it is defended that the "action" propagates at the finite speeds of the pertinent aetherinos (whose average is of the order of V
M) but the direction of the net force is such that "it appears" to propagate at infinite speed (or more precisely, it appears to propagate at a speed much higher than VM).NOTE 5-2
As a comparison consider the case in which at the epoch t of measurement of F
M the direction AB makes an angle j=90º with the x axis and imagine that B has always (in the past) been moving at velocity u in frame S. Then in the reference frame S' associated with B it is A that has all the time been moving at velocity -u . If in this reference frame S' the (incorrect) supposition is made that the action of A propagates at a specific speed c then it must be admitted that the "action" reaching B at t departed A at the epoch t-AB/c when A was yet at a distance AB.u/c further to the right. But if all the action detected by B at t departed A from this earlier position then the force on B at this epoch t should have a direction whose angle with x' is bigger than j=90º by an amount ArcSin[u/c]. Making the supposition that c is of the order of VM, for example c=2.5VM, then this angle ArcSin[u/c]= ArcSin[u/(2.5VM)] can be compared with the values of Table[5-10]. For the case u=VM/3 and j=90º, the table gives 1.57º while the classic suppositions made in this note gives the bigger value of ArcSin[u/c]= ArcSin[1/7.5]= 7.7º. (If it is supposed instead that c is simply equal to VM then an even bigger angle of ArcSin[1/3]= 19.5º would be the aberration predicted by a classic non aetherist theory that assumed that the forces propagate at c).----------------------------------
The modulus of the aetherinical material force suffered by B (which in this section has been considered a "Simple body" with no inner moving structure) is:
F
M = [(FnX - FSX)2 + (FnY - FSY)2 + (FnZ - FSZ)2 ]1/2 [5-12]An example computation has also been made to give an idea of how F
M varies with u and j. It has again been supposed in this computation that nA(v)-sA(v) is the example residual distribution Eq[D-11] presented in Annex D. Table [5-12] gives the values of FM obtained in this calculus (multiplied by 1000):| j=18º | 36º | 54º | 72º | 90º | 108º | 126º | 144º | 162º | |
| u=VM/10 | 1.939 | 1.941 | 1.943 | 1.945 | 1.945 | 1.945 | 1.943 | 1.941 | 1.939 |
| u=VM/3 | 1.81 | 1.83 | 1.86 | 1.88 | 1.88 | 1.87 | 1.85 | 1.83 | 1.81 |
| u=VM | 1.28 | 1.49 | 1.69 | 1.81 | 1.82 | 1.70 | 1.46 | 1.13 | 0.77 |
FM Table[5-12]103
(for u=0 (whatever j), this computation gave 103 F
M = 1.952).
Analysis of the force and acceleration assigned by the Official observer OO.
It was shown in Sections 3 (e.g. see Eq [3-11]) that for the Ideal Observer (for which the aetherinos move at constant speed) the material "free" bodies slow down according to the law:
where
[5-15]
is a constant and u(0) is the speed of the body at the epoch t = 0.
Considering that the real clocks (used by OO) are made of material particles suffering the aether drag and hence slowing down (as seen by IO) according to [5-14] it followed that the so called "Tempo rate law" relating the readings of the IO clocks with those of OO was:
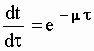[5-16]
But it must be recalled that the negative exponential function of Eq[5-14] was introduced as follows:
The general expression relating the IO acceleration suffered by a composite particle (CP) to the aetherinical force acting on it (see [3-8b]) was:
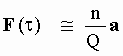[5-17]
and using as F(t) in [5-17] the following expression (see [2-17]) of the aether drag force suffered by a CP in a non shrinking aether:
[5-18]
the following expression was obtained:
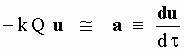[5-19]
that once integrated gives Eq[5-14].
It must be remarked that the expression [5-18] of the aether drag force is an approximation for bodies of "small" speed relative to the aether (i.e. for which u < V
M where VM is the speed for which the aether has a maximum number of aetherinos). Furthermore [5-18] corresponds to a "non shrinking" aether distribution. If instead, it is admitted that the aether distribution shrinks ("cools") slowly in time, then the calculus of the aether drag force will give an expression different from [5-18] and therefore the left hand side of Eq[5-19] will change. In this case Eqs[5-14] and [5-16] will also change.Not being yet evident from experimental or theoretical facts what kind of shrinking must be supposed to occur, the exact quantitative expression of the aether drag force can not be determined. Therefore instead of Eq[5-14] the slow down rate seen by IO in a free body moving in the aether at speed u will (in this section) be written in the more general form:
u(t) = u(0) f(t) [5-20]
and hence the "Tempo rate law" relating the readings of the IO clocks with those of OO will be written as:
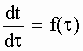[5-21]
What follows is the model's deduction of the acceleration that the Official Observer will attribute to body B. As above, body B moves relative to A and the aetherinical IO forces suffered by B are known. The deduction is similar to the deduction of Newton’s 2
nd law made in Section 4 but now for the more general case in which the aether drag force and the material force (caused by A) have different space directions. The purpose of this deduction is to show that for the Official Observer the aether drag force has no effect. The deduction will be repeated from two different points of view of gradual complexity:(a) The reference frame S of the description is the one associated with the aether (i.e. to the reference frame where the aether can be considered at rest). Body A is at rest in S and exerts a material force on body B. Body B is moving in S with velocity u along the x axis.
(b) The reference frame S of the description is again the one associated with body A but not with the aether. I.e. the aether moves at some velocity V relative to S.
-------------------
(a) The body A and the aether are at rest in the reference frame S of description.
The general expression relating the total aetherinical force suffered by a CP made of n Simple Particles (SPs) to the acceleration that this CP acquires was given in Section 3 (Eq[3-8b]) by:
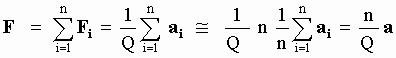[5-22]
The a of [5-22] is the acceleration seen by the Ideal Observer IO. As done in preceding sections, in what follows, the subindex I will indicate a magnitude as seen by the Ideal observer IO and the subindex F as seen by the oFficial observer OO.
Since both observers IO and OO share the same space standards, the velocities uI and uF that they assign respectively to a given body are related by:u
I dt = uF dt = dr [5-23]Therefore from Eq [5-21]:
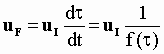[5-24]
The accelerations were defined as:
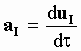
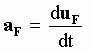[5-25]
It is evident from [5-24] that the IO velocity of a body (or of an aetherino) has the same direction as its OO velocity.
The derivation of both members of the vector equation [5-24] with respect to t gives:
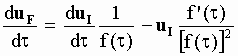[5-26]
multiplying [5-26] by dt/dt , using [5-21] and introducing the accelerations defined in [5-25]:
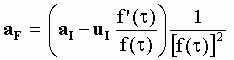[5-27]
Considering that the total aetherinical force acting on B is the vector sum of the material force FM exerted by A and the drag force FD due to the velocity of B through the aether, then, using in Eq[5-27] the general expression [5-22] relating an aetherinical force to the acceleration aI seen by IO:
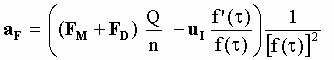[5-28]
Let aID be the acceleration (as seen by IO) suffered by B due only to the aether drag force. (i.e. the total acceleration aI suffered by B, being a vector, can be considered to be the sum of aID plus the acceleration aIM due only to the material force FM exerted by A). aID can be written:
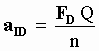[5-29]
but although the exact dependence of the drag force FD on the absolute velocity of B has been assumed (in this section) that it is not known , a relation can nevertheless be found between aID and uI as follows:
The slow down law (as seen by IO) of a "free" body moving through the aether at the absolute speed u has been assumed above to be given by Eq[5-20]. But the scalar equation [5-20] can be generalized to the following vector equation:
u(t) = u(0) f(t) [5-30]
and the drag IO acceleration aID just defined is just the time derivative of the absolute velocity given in [5-30]. Therefore:
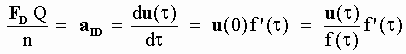[5-31]
But in this example description called (a) the velocity uI of body B in S is also its absolute velocity through the aether. Therefore the u(t) appearing in [5-31] can be equated to uI and therefore using [5-31] , the OO net acceleration of the body B given in [5-28] takes the simple form:
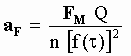[5-32]
where FM is the aetherinical (IO) force suffered by B at the epoch t of observation. But it was noted in section 3 that due to the slow down observed by IO in the internal speed w of the Simple Particles composing A, this material force decreases with time as:
FM(t) = FM(0) [f(t)]2 [5-33]
This relation [5-33] was checked to be true in computations of the force exerted by A on a body B that is at rest relative to it. (The computations were done supposing that the body A was a CP producing a residual distribution of the type [D-11] of annex D, and computing the aetherinical force for several values of the internal speed w of the SPs making A). These computations have been repeated for the case (Fig[5-1]) of a body B now moving relative to A, studying the modulus and direction of the aetherinical force suffered by B for different values of the internal speed w of the SPs making A. This is equivalent to study the dependence of FM with time considering that (for a non shrinking aether distribution) w is all that changes in time as seen by IO. It has been found in these computations that, for small u, the vector generalization of [5-33] is approximately true. I.e.
FM(t) = FM(0) [f(t)]2 [5-34]
Therefore the acceleration seen by the Official observer OO can for the present purposes be written as:
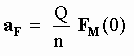[5-35]
which is again Newton's 2nd law (see for example Section 3 and [3-32]).
NOTE 5-3
The interpretation given to the modulus of FM(0) can be found in Section 3. In what respects the direction of FM(0) it is interpreted that it has to be given the same direction of FM(t) which is the force that appears in [5-32] (and that has been calculated above Eqs[5-7]...) because 1/[f(t)]2 is just a scalar factor.
Notice also that if the vector equation [5-34] is not strictly but only approximately true (for small u) this would imply that Newton's 2nd varies in time (also) for the official observer. In any case the range of validity of [5-34] is a second order effect (for large u) whose solution is expected to depend on the type of shrinking (cooling) aether distribution that is introduced in the model and this question has not been solved yet.
But there is another (first order) effect predicted by the model that affects the range of validity of Newton's 2nd law that must be mentioned: The aetherinical force FM(0) (i.e. at t = 0) that the official observer must evaluate to deduce the acceleration aF produced by A on B (at all epochs) depends on the residual distribution of A at the epoch in which the pertinent aetherinos depart A. For example the aetherinos of speed v reaching B at t = 0 emerged from A at the epoch -D/v. It is therefore the values of the distributions nA(v) and sA(v) at this epoch -D/v that affect the number of aetherinos of speed v reaching B at the epoch t = 0. But due to the aether drag slow down of all matter the speeds w of the internal SPs making A are also expected to slow down in time (as has been repeated several times in this work). But the value of these internal speeds w has a strong influence on the values of the distributions nA(v) and sA(v) in such a way that the force that they produce increases with w in a quadratic way. But the bigger the distance D between A and B, the earlier the mean epoch that must be traveled back to single out the distributions that will affect B at t = 0 and therefore faster mean internal SP speeds w will be found at A creating a stronger residual distribution that will later (at t = 0 ) be responsible of a stronger force. This effect supports the point of view of some authors that defend the need to revise Newton's law of Gravitation for large distances to explain some astronomical observations without having to invoke the existence of hidden mass.
--------------------------------
NOTE 5-4
There are some other consequences of the model related with this
section that should be mentioned:
- It was said above that the material force FM represented in Fig[5-2] corresponds to an attraction because the body A
(source of the force being considered) redistributes the aetherino speeds in such a way
that those "scattered" at it had on the average faster speeds v than those
"emergent" from A (after their redistributing collisions). The opposite would be
true for a body A repelling B. But attraction forces (and more specifically gravitation)
are dominant in the Universe. (The repulsion forces that occur in electromagnetism between
equal sign charges are somehow cancelled by a similar number of EM attraction forces
between different sign charges). It can therefore be expected that the average speed of
the aetherinos of the Universe decreases with time (as seen by the Ideal Observer). This
is what has been called a shrinking (or cooling) aether distribution in Section
3. This cooling seems adequate to justify that the physical laws and physical constants
have remained apparently unchanged during millions of years. To understand the idea it
must be remembered that according to the model the aetherinos travel (between collisions
with matter) at constant speed relative to an Ideal Observer but at increasing speeds
relative to us (Official Observers) because our clock mechanisms are slowing down (as
seen by IO) due to the aether drag. In absence of a compensating "cooling" of
the aether (as seen by IO) we, Official Observers, would notice a "heating" of
the aether with time that would imply big changes in our physical laws and/or constants.
- Although an aether of fast moving aetherinos somehow represents an
unlimited reservoir of energy it must also be realized that such energy is only virtual
because (using an analogy with thermodynamics that shouldn't be pushed too far) the
aetherinos are globally in a state of great randomness (or entropy) and somehow in
"thermal" equilibrium with matter. But as seen above, it happens that in their
collisions with attracting bodies the aetherino speeds are on the average redistributed to
lower values (cooling). This suggests that "in compensation" the matter
of those attracting (gravitation-active) bodies should be expected to increase its
energy/temperature. In other words, the gravitation-active bodies are perhaps extracting real
energy from the aether. This phenomenon seems to agree with the predictions and
detailed studies of Paul Stowe that, using his own model of aether, has
for many years been defending the idea that, due to a continuous heating by the aether,
the big planets do in fact radiate more than can be accounted by the mainstream theories
about their formation and their age.
--------------------------------
NOTE: The comments about time dilation due to speed and time dilation du to gravitation that were included here have been modified and moved to Section 1.
Inertial reference frames.
The concept of "rectilinear" reference frame was introduced in Section 1 as an assumed to exist reference frame in which all the aetherinos travel in straight lines at constant speeds. The distance traveled by one given aetherino of a rectilinear frame can be used to define the time (i.e. the clock) associated to the description. Once this aetherino clock is singled out it is the only and absolute clock to be used in all other IO reference frames. But if a rectilinear frame exists, as is postulated, then there exist an infinity of them since any frame moving at a constant velocity relative to the first is also a rectilinear frame. The absolute clock just mentioned is the clock that defines the absolute time for the Ideal Observer's description and it is in reference to this clock that the velocities relating the rectilinear frames may be considered constant. The Official Observers OO instead use their own absolute time according to which the aetherinos of the rectilinear frames no longer move at constant speeds but at speeds that increase as vF=vI /f(t). Furthermore if S and S' are 2 rectilinear frames, an Official observer sitting at S and using its OO clock, will see that S' moves relative to S at an increasing speed given again by V=V(0)/f(t). As can be inferred from Section 1 it is believed that any standard material clock (e.g. atomic, pendulum, based on the Earth's rotation, etc,...) will (under "normal" physical conditions) see the aetherinos increase their speeds according to the same law V=V(0)/f(t) due to the fact that all matter (including the subatomic particles and therefore the atomic clock "mechanism") slows down for IO at the same (simple exponential) rate due to the aether drag force. Therefore in principle any standard material clock can be used as the one and only clock to define the absolute time for the Official Observer description in any frame.
An inertial reference frame is defined (in mainstream physics and in this model) as a reference frame in which the law of inertia (Newton's 1st law) holds. This constancy of velocity of a body "free" of material forces will only happen for the Official observer for which the slow down due to the aether drag is hidden due to the behavior of his clocks. For the Ideal observer instead, a "free" body moving through the aether slows down (according to his clocks) due to the aether drag. All material bodies "free" of material forces (including gravitation) define therefore an inertial frame for the Official observer even if they move relative to the aether.
The aether "rest" frame, i.e. the reference frame in which the aether can be considered to be at rest (at least in the locality of the experimenter) is also an inertial reference frame. This rest frame is also a rectilinear frame for IO but all other rectilinear frames move with respect to the rest frame at a constant IO velocity and therefore are not inertial frames because no "free" body, defining an inertial frame, moves at constant IO velocity relative to the local rest frame (due to aether drag slow down). This implies, that the aetherinos do not move in straight lines in the inertial frames (except those aetherinos that move along the direction of the inertial frame's velocity relative to the aether rest frame). The curvature of the aetherino trajectories in an inertial frame will nevertheless be small for the aetherinos of high speed (specially if the speed decrease observed by IO in the "free" bodies is small).
It is straightforward to show that for the Official observer the velocity of a free body relative to any other free body is constant. This will prove that the model's association of a free body with an inertial frame is consistent with the mainstream definition since it will happen that the inertial frames thus defined have a constant velocity relative to any other inertial frame.
In two space dimensions (without loss of generality) the IO velocity components of an inertial frame A would be given by
VAX(t) = VAX(0) f(t)
VAY(t) = VAY(0) f(t)
and those of the velocity of another inertial frame B by:
VBX(t) = VBX(0) f(t)
VBY(t) = VBY(0) f(t)
Therefore, according to the Galileo transformation (t being an absolute time), the velocity assigned by IO to the frame B as seen from reference frame A is:
vABX = VBX(t)-VAX(t) = [VBX(0)-VAX(0)]f(t)
vABY = VBY(t)-VAY(t) = [VBY(0)-VAY(0)]f(t)
but if the observer is the Official observer and uses its Official clocks he sees any IO velocity as vF = vI dt/dt = vI /f(t) and in particular, sitting at A he sees the velocity of frame B to be:
vABXF = vABX / f(t) = VBX(0)-VAX(0)
vABYF = vABY / f(t) = VBY(0)-VAY(0)
When evaluating an Official acceleration aF , the frame of description will normally be an inertial frame. Therefore care must be taken to account for this fact if the calculus leans for simplicity in magnitudes related to a rectilinear frame instead of an inertial frame.
------------------------------------
(b) The reference frame S of the description is again the one associated with body A but not with the aether. I.e. the aether moves at some velocity V relative to S.
Since the expressions of the aether drag and the material forces were deduced for a rectilinear reference frame (in which the aetherinos move in straight lines) the reference frame S is taken to be a rectilinear frame.
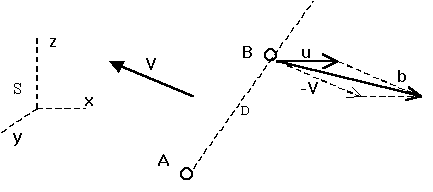Fig[5-40]
V is the velocity of the aether in the reference frame S of description. I.e. the aetherino velocities distribution is isotropic at all speeds in a reference frame that moves at the velocity V with respect to S. It is perhaps V that can be called "the aether wind" in S.
u is again the velocity of body B in S.
b is the velocity of body B with respect to the aether. Therefore:
b = u -V [5-40]
As usual the subindexes I and F will be used to denote the magnitudes seen respectively by the Ideal and oFficial observers. Therefore the velocity of the body B relative to the aether will be written as:
bI = uI -VI (for the ideal observer IO) [5-41]
bF = uF -VF (for the official observer OO) [5-42]
(The relation between an IO velocity value and its respective OO value was given for example in Eqs[5-23..24], the equations being valid not only for u but for any velocity like for instance V and b).
Following now the same steps of deduction (a) to obtain the acceleration aF assigned by the official observer to the body B subject to the material force exerted by A, (see Eqs[5-20...35]) and considering that uI = uF dt/dt = uF f(t)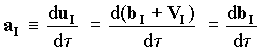
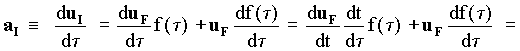
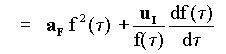
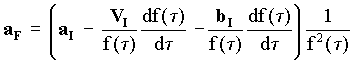[5-46]
but since the net aetherinical force acting on B can be written as the vector sum of the material force FM and the drag force FD , using the Eq[5-22]:
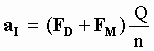[5-47]
but, see Eq[5-31], the aether drag force FD acting on B is related to its absolute velocity bI through the aether by:
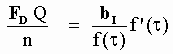[5-48]
and therefore using [5-47] and [5-48] in [5-46]:
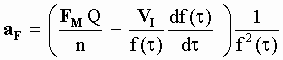[5-49]
The expression [5-49] corresponds to the acceleration of the body B observed by the official observer in the rectilinear frame S. But this official observer is interested in descriptions referred to inertial frames, not to rectilinear frames. The inertial frames have been shown above to accelerate relative to the rectilinear frames. Let SL be the inertial frame that at the epoch t0 of description has the same velocity as the rectilinear frame S.
In this case an Ideal observer sitting at ST (using ideal clocks) sees the rectilinear frame S move relative to it at a speed VSI = VI - VI . f(t)/f(t0) in the opposite direction of the aether wind VI. An Official observer (using official clocks) , sees the rectilinear frame S move relative to it at a velocity (see for example [5-24])
VSF = -VSI / f(t) = -VI.[1/ f(t)-1/ f(t0)] [5-50]
this implies that at the OO acceleration of S relative to the inertial frame ST is:
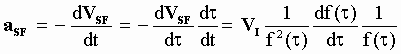[5-51]
The acceleration of B seen by the Official observer in an inertial frame of description is finally (see Eq[5-49]):
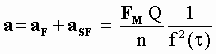[5-52]
which is again the same expression of [5-32]. Therefore in both calculi (a) and (b) the dependence of the aether wind disappears explicitly for the Official Observer in his descriptions of the acceleration suffered in an inertial reference frame by a body B.
Centripetal acceleration.
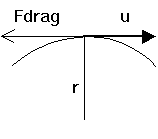
Fig[5-55]
Let u be the instantaneous velocity of the body relative to the aether. The body is describing a circular trajectory of radius r.
Suppose first for simplicity that u is the velocity of the body relative to the aether (i.e. the reference frame of description of Fig[5-55] is the one associated to the local rest aether). The Official acceleration aF of the body is related to its Ideal acceleration aI by :
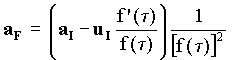[5-56]
as was deduced above (see Eq[5-27]). In the absence of the body A (and of its material force) the Ideal acceleration a
I is now made by the sum of the acceleration due to the aether drag and the centripetal acceleration observed by IO. Therefore: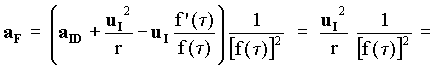
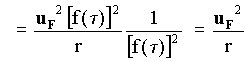[5-57]
where [5-31] and [5-24] have been used. The main point of this analysis is again to show that for the Official observer the aether drag force disappears.
From the point of view of the Ideal Observer, the centripetal acceleration of a body describing an orbit of radius r with a velocity uI is given by (see 5-30):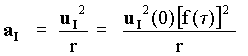
[5-58]
The requirement that the model must be consistent with the existence of stable orbits (atoms, planets) does not seem to pose further problems. Notice that whatever the rate of the official clocks relative to the ideal ones (i.e. whatever the form of the function f(t) that makes possible a consistent description) it seems that the stability of orbits is, a priori, allowed if the aetherinical "material" forces behave as has been said (see 5-34). For a given orbital radius r, the orbiting body slows down in time for IO and therefore its centripetal acceleration decreases but the aetherinical material force produced by the "central" body does also decrease in time for IO at the same rate, and therefore the equilibrium of the centripetal and centrifugal forces occurs at the same radius i.e.
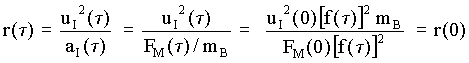
where
mB is the mass of the orbiting body and FM is the material force exerted on it by the attracting body.If the description reference frame (Fig[5-55]) is not the one associated to the aether at rest and therefore u is no longer the velocity of the body relative to the aether, the same reasonings of the example (b) can be made (see above) and it will again be predicted that the aether drag force does not enter the expression of the centripetal acceleration when the Official observer describes it from an inertial reference frame.
Discussion about a principle of relativity.It has been shown above that, according to the model, for a given material force FM acting on the body B the OO acceleration aF does not depend on the inertial reference frame of description. It has also been shown that for a given material force FM , the acceleration does not depend explicitly on the speed uF of the body relative to the aether. It does depend implicitly on this speed uF due to the dependence of the mass of the body B on its absolute speed. To be consistent with what are being considered experimental facts it remains to show that the force FM suffered by B due to the presence of A does not depend on the velocity of these bodies relative to the aether but only on the "relative configuration" of A and B. This configuration is a priori expected to depend not only on the relative position but also on its time derivatives. (E.g. in electromagnetism the total (electric + magnetic) force suffered by a charge B due to another charge A depends not only on the relative position of A and B but also on their relative velocity). If A is at rest in the aether it is evident that its residual redistribution is isotropic and therefore the force FM suffered by B will only depend on the "relative" configuration of the interacting bodies. But if A moves through the aether it is expected that its residual redistribution will no longer be isotropic and therefore that the force FM suffered by B will no longer depend on the "relative" configuration of these bodies but on their "absolute" space configuration (i.e. will depend on the direction of AB relative to that of the aether wind). It seems possible that, for small absolute speeds of A an apparent principle of relativity affecting all material forces may be predicted. The range of validity of such approximate principle may be inferred from a mathematical treatment of the redistribution process, similar to the one presented in annex D, but now introducing a dependence on direction in the probability of emergence of the colliding aetherinos. Assuming that the Earth moves at about 400 Km/s relative to our local aether (as suggested by the studies of the dipolar anisotropy in the background microwave radiation), it can be ascertained that known experiments have detected no violation in the principle of relativity in reference frames of absolute speeds of the order of 400 Km/s (i.e in 0.13 % of c, which is a rather small speed for aetherino speed standards). It does seem plausible that the model can account for these limited range experiments, but this study is not available in this version of the work. What the model should demonstrate is that, supposing that A moves at 400 Km/s relative to the local aether, the aetherinical material force FM varies with the direction of B at most in a quantity K which is smaller than the power of resolution of the accepted experiments.
From a strict point of view, the prediction of the model is that the so called "restricted" principle of relativity does not hold.