Radiation emitted by electrons.
P.S. Nov 2010. A new and more complete version of this paper is now radiations_en.pdf
----------------------------
This is a preliminary, qualitative and speculative sketch of how the aether model can interpret the radiation emerging from the electron in some scenarios. Examples of these scenarios are the following:
* Circular orbiting in a uniform magnetic field and "synchrotron radiation".
* Central force and electron orbiting a nucleus.
* Rectilinear acceleration and "bremsstrahlung".
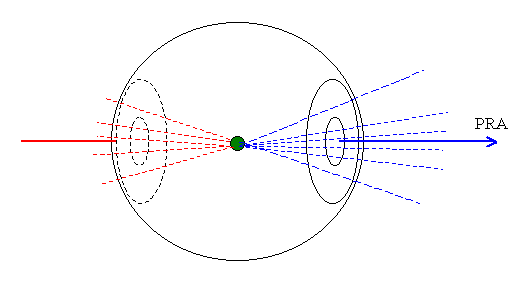
As said in other sections of this work it is assumed that the electron is a composite particle that redistributes the speeds of the aetherinos that collide with it. But it is supposed that, even when the electron suffers no acceleration, this redistribution is not isotropic relative to the electron but has instead a "preferred redistribution axis" (PRA). See Fig(R-1). On the other hand, the global redistribution of a numerous group of non accelerated electrons whose preferred redistribution axis are randomly aligned in all directions of space can be considered isotropic relative to the group as a whole.

Fig (R-1)
Proposed geometry of the symmetry in the redistribution of aetherinos by an electron. (It must not be confused with a geometry of emission of radiation. The aetherinos are not radiation, but the features of radiation are implemented by the periodicities in the distribution of aetherinos reaching the detector).
The PRA of an electron will spin (rotate) in space under given circumstances (e.g. when the electron is bathed by some non uniform shower of aetherinos). The vector characterizing the rotation rate of the redistribution axis will be called intrinsic rotation vector (IRV).
Suppose that, during a small time interval dt, the electron's redistribution axis PRA rotates a small angle dq (i.e. if it was pointing to some space direction A1 it tilts to point to some new direction A2). As usual in the description of rotations, the vector (IRV) representing such rotation rate is agreed to be a vector perpendicular to the plane formed by A1A2, pointing in the semi-direction of a screw that turns clockwise A1 over A2 and with a modulus equal to the time rate dq/dt (angular speed). See Fig(R-2).
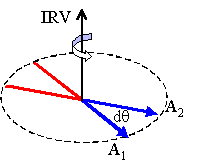
Fig (R-2) In Fig (R-2), the preferred axis of redistribution of the electron is represented by a vector with a blue head and a red tail. The figure represents such PRA in two different orientations. In changing from the orientation A1 to the orientation A2 the PRA performs a rotation. Its rate of rotation is represented by the up-pointing vector IRV.
Some puzzling facts about the radiation emitted by electrons can perhaps be qualitatively understood supposing that:
- An electron that moves in an inertial reference frame with constant velocity remains with its preferred redistribution axis pointing in some direction, i.e. its PRA does not rotate (except perhaps for some small random rotations due to the randomness of the aether).
- As is well known, an electron that moves perpendicularly to a uniform magnetic field suffers a force (the Lorentz force) that compels the electron to describe a circle (of decreasing radius) in a plane perpendicular to the magnetic field. Therefore the electron undergoes an acceleration. Due to the combined effect of the magnetic field and such acceleration, the electron is bathed by a specific, non-isotropic, shower of aetherino collisions that forces the "preferred redistribution axis" of the electron to rotate in space (due to aetherinical forces1 that have not been studied yet). The experimental facts about the radiation emitted by the electrons suggest that, when an electron performs such magnetically-compelled circles, the intrinsic rotation vector of the electron aligns itself at all times with the centripetal acceleration. See Fig(R-3). Furthermore, if the electron travels along the circle at non relativistic speeds, the experimental facts suggest that the modulus of the IRV is equal to the angular speed of rotation of the electron along its circular trajectory. If the electron travels in curved trajectories at relativistic speeds (e.g. in a high energy synchrotron) the angle of observation of the electron has a great influence in the frequency of the radiation detected due to the great influence that has the Doppler effect in such cases. (Along the "short" arc of the electron's trajectory visible at the radiation window their velocity makes different angles with the direction of observation. The wide span in frequency of the synchrotron radiation can, for relativistic electrons, be explained by only small variations in such angle). On the other hand, the fact that the intensity of synchrotron radiation is significant only at very small angles above and below the plane of motion (high collimation) together with the fact that the radiation is polarized in the plane of motion suggests that for electrons "circling" at relativistic speeds their IRV is no longer aligned with their acceleration but is instead aligned perpendicular to the plane of motion (plausibly the IRV of the electrons being anti-parallel to the angular velocity vector of their curved trajectory).
-
When an electron performs an orbit due only to the attraction of a central charged body, e.g. when it orbits a nucleus, it is known that the electron does (normally) not radiate. This case can be implemented supposing that in those orbits the PRA of the electron remains aligned at all times in a direction perpendicular to the plane of the orbit. The aetherinical distribution (implementing the central "electric field") produced by the charged nucleus would be responsible of this alignment. An observer placed at a distance much bigger than the average radius of the electronic orbit and looking at the electron will always see the same angle between the direction of observation and the PRA of the electron and will therefore not detect any periodically varying aetherino distribution (radiation). (Note: due to the different speed of the electron relative to the observer in the different positions of its orbit, the distant observer will actually notice a weak periodic variation of the aetherino distribution but this radiation will be negligible if the orbital speed of the electron is much smaller than c, if the hypothesis c+ governs the detection and/or if the aetherinical redistribution created by the electron is only strong at small angles relative to its preferred redistribution axis).- When an electron is fired towards a heavy target or against a stopping electric potential it suffers a deceleration. Consider here only those parts of the trajectory in which the acceleration (deceleration) vector is approximately parallel to the electron's velocity. It can be said that it there suffers a "rectilinear" acceleration. The thesis is again that, during a rectilinear acceleration, the PRA of the electron is forced to rotate with its IRV aligned with the acceleration of the electron and such that the modulus of the IRV increases when the modulus of the electron's inertial acceleration increases. This alignment "explains" that an external observer detects radiation mainly along directions perpendicular to the acceleration (or close to them). See Fig(R-4)
------------------
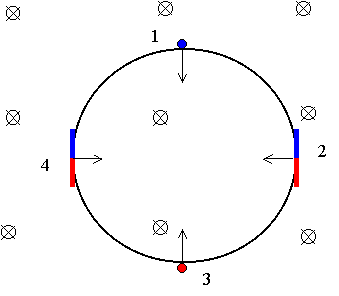
Fig (R-3)
Fig (R-3) represents the circular trajectory of an electron in a uniform magnetic field. The electron travels clockwise in the figure (passing successively by the positions 1-2-3-4-etc). In the example, when the electron is at position 1, its PRA is perpendicular to the plane of the trajectory and pointing towards the reader (blue point). But the PRA is spinning and when the electron passes by position 2 its PRA is now tangent to the trajectory and pointing "up" as seen by the reader. The intrinsic rotation vector IRV (representing the rate of rotation of the electron's PRA) is represented by the arrows. When the electron passes position 3 its PRA is pointing away from the reader and is again perpendicular to the circle. At position 4 the PRA is again tangent to the trajectory. An external observer, like for instance the reader, detects a radiation because he detects a periodically varying aetherino distribution (e.g. suppose that a bigger number of aetherinos emerge from the electron in semi-directions that make a small angle with its blue semi-direction than in the opposite semi-directions; or suppose for example that the aetherinos emerging close to the blue semi-direction have higher speeds than those emerging close to the red one).
------------------
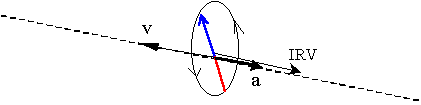
Fig (R-4)
Fig (R-4) represents an electron being forced to decelerate whose acceleration "a" is parallel and opposite to its velocity "v". The same aetherinical force that produces the electron's deceleration is considered responsible of feeding a rotation on the electron's PRA whose rotation vector IRV is parallel to "a".
------------------
The model of the aether proposed in this work defends that light (and radiation in general) is a wavelike disturbance that alters the distribution of aetherinos (or more precisely the distribution of their velocities). The apparently corpuscular behaviour of light in some scenarios can plausibly be explained in a simple way by the cooperative effect of the pertinent aetherinos without invoking the controversial concepts of "photon" and "wave collapse". Section 6 of this work gives hints of how to explain some of these phenomena.
The following feature of the emission of synchrotron radiation seems at first sight difficult to explain within a pure wave model of light: How can the electrons emit "a wave" during the short time of their passage in front of a window of the storing ring? How can the electrons, that when in front of the window all they do is follow a simply curved trajectory, create at that time thousands of radiation wave fronts?. The proposed explanation is as follows:
When an electron follows in a synchrotron a curved trajectory it is being accelerated (by the bending magnets). As said above, in these circumstances the "preferred redistribution axis" (PRA) of the electron is spinning with an intrinsic rotation vector (IRV) aligned with the electron's acceleration. Its PRA is therefore spinning in a plane perpendicular to the plane of motion of the electron. During the short time that an electron is in front of the radiation window its PRA will rotate say q radians. As explained below, this angle q needs not amount to many turns. It can be a small fraction of a single turn (i.e. a small fraction of 2p radians). Suppose that the anisotropic redistribution of the electron (Fig R-1) can be characterised by a sine function (for example suppose that along one of the semi directions of its PRA emerges an excess number of fast aetherinos and a deficit of slow ones while along the opposite semi direction emerges a deficit of fast aetherinos and an excess of slow ones, and suppose that there is a sinusoidal evolution of the redistribution as the angle of emergence of the aetherinos increases relative to one of the former preferred semi directions. This is a deliberately vague example of redistribution, the details not being important in this context). Each electron "i" of the bunch will appear in front of the window with its PRA making some particular random angle a(i) with the direction to the observer and will disappear from the window with the new angle a(i)+q. Each electron contributes to the "total" disturbance with just a small fragment of a sinusoidal wave of "length" q and random phase. (The so called "total disturbance" is the complete disturbance received by the observer as a consequence of the passage of a whole bunch of electrons in front of the radiation window). Let Dt be the total time during which the bunch of electrons is passing in front of the window (i.e. if the first electron of the bunch appears at the window at t1 and the last disappears from in front of the window at t2 then Dt=t2-t1). Each electron of the bunch will appear in front of the window at some particular random epoch t(i) (such that t1£ t(i)< t2 ) and since all the electrons of the bunch have the same speed they will all spend the same time Dt to cross the arc of trajectory in which they are visible at the window. Therefore the ith electron disappears from behind the window at the epoch t(i)+ Dt. It can be seen in a simulation that the sum of a big number of fragments of sinusoidal waves of equal2 frequency, random phase, random start t(i) and equal duration Dt is indeed a sinusoidal wave of the same frequency to that of the fragments (provided that the number "n" of electrons of the bunch is n >> Dt/Dt). The following screenshot of an evaluation done with Wolfram's Mathematica shows an example of that assertion:
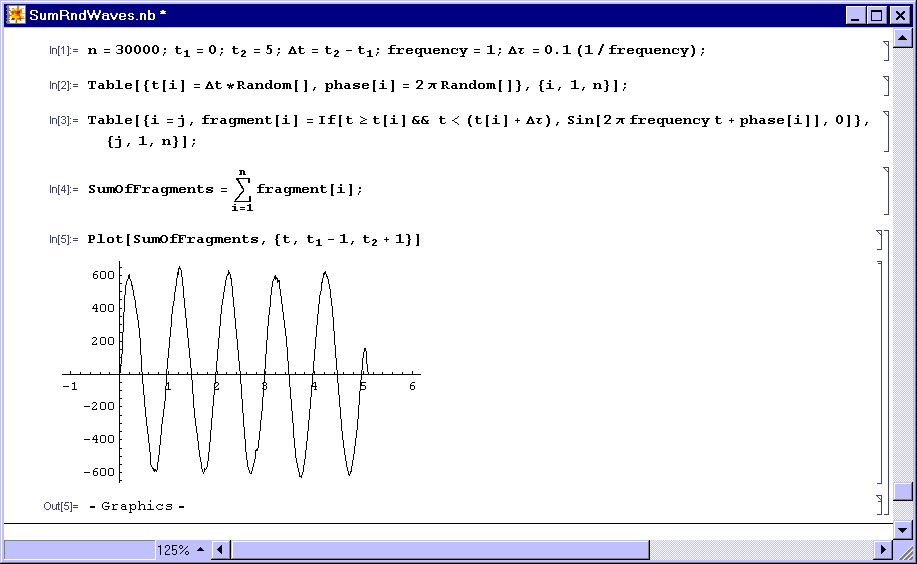
To be completed when possible.
P.S. Nov 2010. A new and more complete version of this paper is now radiations_en.pdf
Footnotes
1 The plausible internal structure of the electron has not been modelled yet. For many purposes (e.g. when the electron is the target of aetherinical forces) the electron is being treated along this work as a Simple Particle. But from a strict point of view the electron can not just be a Simple Particle because the electron originates an aetherinical redistribution. It seems plausible that the electron can be satisfactorily modelled by some association of two or three Simple particles that orbit each other in some specific way.
The frequency of the sinusoidal wave from which the fragments are cut is equal to the modulus of the IRV but applying to it the Doppler effect due to the fact that the electrons are travelling at high speed towards the observer.