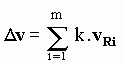 [M-1]
[M-1]ANNEX M
Abstract: A material force is introduced in the second part of the Annex and the new acceleration observed by the Ideal Observer is deduced. The Official observer will also notice in this case that the particle accelerates. Finding this expression of the OO acceleration is the main purpose of this Annex since with it the model's fundamental law of dynamics can be enounced (relating a real force with the real acceleration that it produces as a function of the absolute speed of the body relative to the aether). From this law, expressions for the momentum and the kinetic energy of massive particles should next be deduced. |
In Section 3 of this work it was postulated that when a material Simple Particle (SP) suffers the impact of an aetherino it increases its velocity by an amount k.vR where k is a constant and vR is the velocity of the aetherino relative to the SP. (Note: this constant k corresponds to the product of the two constants q and Q used in Section 3).
Suppose that during a small time interval Dt the SP suffers the collisions of m aetherinos with relative velocities vR1, vR2, … vRm Then, at the end of Dt the SP has suffered a net velocity change given by:
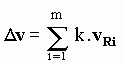 [M-1]
[M-1]
and it happens that, if at the beginning of the time interval Dt the SP had a velocity (in the reference frame of description) equal to zero, at the end of that interval it has a velocity Dv. But it maintains this velocity Dv only during a very short time (at the end of Dt, after suffering its last collision) and just until it suffers the next aetherino collision. This velocity Dv is (in general) not representative of the macroscopic velocity change suffered by the SP during that time interval Dt. The "instantaneous" velocity of the SP fluctuates and is by itself of little interest to describe the movement of the SP. The model is interested in describing the macroscopic velocity change with time of a SP suffering a given "macroscopic" aetherinical force.
- - - - - - - - -
NOTE: An aetherinical force suffered by a material particle has been defined as the net aetherinical impulse per unit time. It could then in principle be evaluated adding the impulses received by the SP during a small time interval Dt and dividing such net impulse by Dt. But imagine a theoretical very sharp observer that is aware of every single collision suffered by the particle; then if this observer makes several evaluations of the force relying on time intervals so small that the number of collisions that it includes is also small, he will report that the value of the force fluctuates in time. It can be said that such observer is describing a microscopic aetherinical force. Instead the force can be considered (and called) macroscopic if it has "the same" value when evaluated using time intervals "big enough" for a statistically significant number of aetherino collisions to occur. Or better still, the macroscopic aetherinical force acting on a SP will be considered to be the average of the forces measured over a big number of SPs in similar conditions. Notice that it is the number of collisions (and not necessarily the Dt used for its evaluation) that needs to be big to allow the force to be considered macroscopic. Therefore, if the particle suffering the force is composed of a very big number of Simple Particles, it will also receive on the whole a very big number of aetherino collisions even during a much smaller Dt and the fluctuations of such global force can also be neglected.
But, even if it is agreed that the concept of "macroscopic aetherinical force" is useful for the theoretical development of this aether model, the discontinuous microscopic nature of the aetherinical impulses must not be neglected because, as will be shown below, it has important implications on the laws of movement of the material particles that a classic continuous force concept can not account for. For example suppose a SP initially at rest at x = 0. If the SP is subject to an aetherinical force, its position x will show a big dispersion of values after a long time interval (specially if the constant k mentioned at the beginning of this Annex is not too small). On the other hand a "composite" particle made of a big number of SP (but otherwise immersed in the same specific environment of aetherinos) will show a much smaller dispersion of positions after the same time of observation and it can be said that its behavior is more "classic". (When referring to the "dispersion" of positions it must of course be understood that the experiment is made many times with the particle in the same initial conditions and suffering the same average aetherinical force during the same time interval). But it is not the purpose of this Annex to make an exhaustive study of how can the basic phenomena of Quantum Mechanics be modeled with the statistics of aetherinos.
- - - - - - - - -
The following calculus deduces the macroscopic (average) velocity of a SP subject to an aetherinical force taking into account the microscopic properties of such force.
The first part of this calculus will be described as if it happened in one (space) dimension (i.e. the SP and all the pertinent aetherinos colliding with it, are imagined to move, in the reference frame S of description, along a direction X). The term "velocity" will be used (instead of "speed") to account also for the semi direction +X or –X along which move the pertinent aetherinos and the SP. The result can be generalized to a 3D space considering that it can be applied to the component of all the aetherino velocities along the pertinent direction which is the direction of the initial velocity of the SP through the aether. (The impulses, accelerations, etc…, along the other two orthogonal space components average to zero).
Suppose that the SP suffers an ordered sequence of m collisions such that the velocities in the frame S of description of the m aetherinos that collide one after the other with the SP are respectively v1, v2, …,vm
Since when a material Simple Particle suffers the impact of an aetherino it increases its velocity by an amount k .vR where vR is the velocity of the aetherino relative to the SP, then, if the SP has a microscopic velocity in S equal to Vi and is collided by an aetherino of velocity in S equal to v (and therefore of relative velocity v –Vi ), the SP will change its S velocity from Vi to Vi + k (v –Vi). More generally it will be written:
![]() [M-3]
[M-3]
to express the microscopic velocity Vi of the SP after suffering the collision of an aetherino whose velocity in S is vi and where Vi-1 is the velocity of the SP previous to this collision.
With the initial condition that (before the sequence of m collisions being computed) the microscopic velocity of the SP was V0 it can be seen by application of [M-3] that after the mth collision of an ordered sequence of collisions of aetherinos of velocities in S respectively v1, v2, …,vm , the instantaneous microscopic velocity of the SP is equal to:
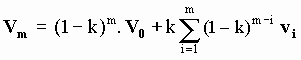 [M-4]
[M-4]
Such instantaneous velocity (after the mth collision) depends not only on the velocities of the aetherinos that have collided with the SP but also in the order in which these m aetherinos collide (i.e. Vm will in general be different if the order of collisions is given for example by v2, v1, v3, …,vm instead of by v1, v2, v3, …,vm). If it is then supposed that the m aetherinos can collide with the SP in any possible order (i.e. that all the m! permutations of {v1, v2, v3, …,vm} are equally probable) it can be calculated that, averaging Vm for all the m! possible permutations of collisions, the average instantaneous velocity of the SP after the mth collision is:
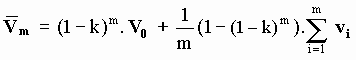 [M-5]
[M-5]
Suppose now that the frame S of description (in reference to which are given the velocities of the colliding aetherinos) is the one that can be associated with the undisturbed aether at rest. It will be calculated an expression for the time evolution of the speed of a SP that is released moving at initial speed V0 in such undisturbed aether. The speed will be seen to slow down in time for the Ideal Observer (that uses ideal clocks) due to the non symmetric impacts of aetherinos suffered by the SP.
It will be of interest, see below, to evaluate [M-5] choosing a number m of aetherino collisions equal to the average number Y of them occurring in unit time. This average number was calculated in earlier sections of this work as follows:
Suppose that in the reference frame S (associated with the aether at rest) the speed distribution of aetherinos in 3-D space is given by:
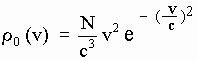 [2-19]
[2-19]
as in Eq[2-19] of Section 2, where c is just the speed for which such distribution reaches its maximum.
(Note: it is not claimed that the speed of light is the same as the speed for which the aether_at_rest distribution reaches its maximum).
Following the same line of calculus of Section 2, the number of aetherinos that collide in unit time with a SP moving at speed u through the aether is:
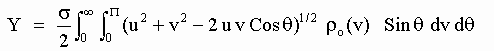 [M-6]
[M-6]
where s is the geometrical cross section of the SP.
Eq[M-6] is the same as Eq [4-4] and , as it was said in Section 4, it can be partially integrated giving:
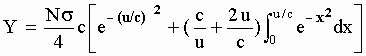 [M-6b]
[M-6b]
The factor 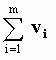 that appears in [M-5] must be
interpreted in this 3-D case as giving the sum of the x components of the
velocities (referred to S) of the m colliding aetherinos. But, since the number m
of collisions in [M-5] will be taken equal to the average number Y of them occurring in
unit time, the sum
that appears in [M-5] must be
interpreted in this 3-D case as giving the sum of the x components of the
velocities (referred to S) of the m colliding aetherinos. But, since the number m
of collisions in [M-5] will be taken equal to the average number Y of them occurring in
unit time, the sum 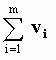 can consistently be
approximated adding the x components of a statistical sample of the aetherinos that
collide with the SP also in unit time. This can be calculated with the following
integration:
can consistently be
approximated adding the x components of a statistical sample of the aetherinos that
collide with the SP also in unit time. This can be calculated with the following
integration:
Recalling again the calculus made in Section 2, an aetherino that has in S a direction q and speed v, has a velocity whose component along the direction of the velocity u of the SP (here called direction x) is equal to v. Cos(q). Adding these x-components for all the aetherinos that collide with the SP in unit time:
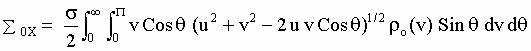 [M-7]
[M-7]
where a sub index 0 has been used in the name S0X (given to such sum of x-components) to remark that here the calculus corresponds to only the aether drag force but zero material force.
[M-7] can also be "partly" integrated giving:
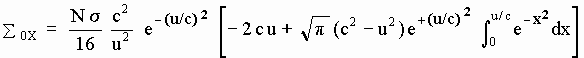 [M-7b]
[M-7b]
If in [M-5], the number m of aetherinos colliding with the SP is taken equal to the average number Y of the aetherinos that collide in unit time with a SP of initial velocity V0, then the acceleration of the SP can "somehow" be expressed as:
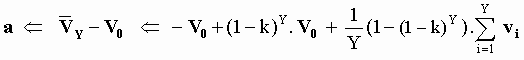 [M-8]
[M-8]
Note: considering that the average microscopic (or instantaneous) velocity of a SP is also its average macroscopic velocity then a is the average increase in unit time of the macroscopic velocity of the SP which will also be called its average macroscopic acceleration.
Substituting V0 by u which is the letter used in other sections for the speed of a SP through the aether, and doing some factoring, [M-8] can be rewritten (in a non vector form) as:
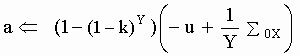 [M-8a]
[M-8a]
Notice however that the right hand sides of [M-8] and [M-8a] are dimensionally
inconsistent to be considered an acceleration. The above calculus of [M-5] was done
assuming (consistently) that m was a dimensionless quantity (i.e. just a number
of collisions). But later this dimensionless number has been equated to the Y given
in [M-6] that is a number of collisions per unit time. Similarly, the 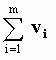 of [M-5], with dimension of speed has inconsistently
been replaced by S0X , with dimension
of acceleration. The dimensionality of [M-8a] can be "repaired"
multiplying both Y and S0X by some
fundamental constant tC of the Ideal
Observer with the dimension of time and dividing the whole expression also by tC. Some subtleties (that will not be yet
discussed) recommend to introduce such constant tC
as the quotient of some fundamental length L0 by the speed c for
which there is a maximum of aetherinos in the local rest aether distribution. This
constant tC = L0/c
will be considered the time unit of the Ideal Observer IO. Hence it will from now on be
supposed that the Ideal Observer defines its unit of time as the time interval taken by
the more abundant aetherinos of its aether at rest distribution to traverse some
fundamental distance L0 considered its length standard. (In
Section 1 it was instead suggested that IO could in theory pick at will a single
specific aetherino to define with it its time unit as the time interval to traverse some
specific distance). Regarding L0 it could be any well specified
distance agreed with the official observer OO with which IO shares its length standard,
like for instance the rigid meter rod of Paris. It is recognized that this
"reparation" is very unorthodox and controversial but it is so far the only way
that has been found to deduce a consistent expression for the macroscopic acceleration of
a particle based on microscopic considerations about its jiggling due to single
aetherino collisions. By "reparation" of [M-8a] the acceleration of the particle
can be written as:
of [M-5], with dimension of speed has inconsistently
been replaced by S0X , with dimension
of acceleration. The dimensionality of [M-8a] can be "repaired"
multiplying both Y and S0X by some
fundamental constant tC of the Ideal
Observer with the dimension of time and dividing the whole expression also by tC. Some subtleties (that will not be yet
discussed) recommend to introduce such constant tC
as the quotient of some fundamental length L0 by the speed c for
which there is a maximum of aetherinos in the local rest aether distribution. This
constant tC = L0/c
will be considered the time unit of the Ideal Observer IO. Hence it will from now on be
supposed that the Ideal Observer defines its unit of time as the time interval taken by
the more abundant aetherinos of its aether at rest distribution to traverse some
fundamental distance L0 considered its length standard. (In
Section 1 it was instead suggested that IO could in theory pick at will a single
specific aetherino to define with it its time unit as the time interval to traverse some
specific distance). Regarding L0 it could be any well specified
distance agreed with the official observer OO with which IO shares its length standard,
like for instance the rigid meter rod of Paris. It is recognized that this
"reparation" is very unorthodox and controversial but it is so far the only way
that has been found to deduce a consistent expression for the macroscopic acceleration of
a particle based on microscopic considerations about its jiggling due to single
aetherino collisions. By "reparation" of [M-8a] the acceleration of the particle
can be written as:
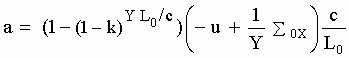 [M-8b]
[M-8b]
[M-8b] is interpreted to give, for the Ideal Observer, the acceleration of a Simple Particle moving through an undisturbed aether (in absence of any other material force) as a function of its speed u relative to the aether (i.e. relative to the reference frame S in which the aether can be considered at rest) where Y and S0X are given respectively in [M-6] and [M-7], k is a dimensionless constant, c is the speed for which there is a maximum of aetherinos in the local aether distribution and L0 is a constant with dimension of length..
- Consider now the case in which the SP, besides moving in relation to the aether, is also under the influence of a material force (i.e. the local aether of the particle is now "disturbed" by the presence of some matter that redistributes the velocities of "some" of the aetherinos).
It will only be analyzed here the simple case in which the direction joining the matter (subject of the force) with the SP (target of the force) is the same as the direction in which the SP is moving relative to the aether.
The calculus will be done just plugging in [M-8] the adequate quantities for this case:
Considering that in this model the so called "material forces" are produced by some matter that only redistributes the speeds of the aetherinos that collide with (but is neither a source nor a sink of aetherinos) it can be supposed in a first approximation that a SP subject to a material force suffers the same net number m(u) of collisions by unit time that it would suffer in absence of the influencing matter but otherwise moving at the same speed u relative to the aether.
In relation to the other term 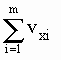 that must also be plugged in Eq[M-8], but now for a SP suffering a material
force, consider the following:
that must also be plugged in Eq[M-8], but now for a SP suffering a material
force, consider the following:
An aetherinical material force suffered by a target particle is being described in this work adding the impulses from those aetherinos that are in excess and subtracting the impulses from those other aetherinos that are in deficit, where the "excess" and "deficit" is in relation with the number of aetherinos of the corresponding speed that would collide with the target particle if it was alone in an undisturbed aether. For example a material force on a Simple Particle at rest in the aether can be expressed by:
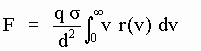 [M-9]
[M-9]
where r(v) is the so called "residual distribution" produced by the matter source of the force. Such distribution r(v) gives the difference between the number of aetherinos of speed v by unit speed interval, by unit time and by unit solid angle, that emerge from the source matter and the corresponding number that would emerge from that volume of space if the matter was not there.
It has not yet been studied in this work how the redistribution produced, for example, by a proton changes when the proton moves relative to the aether. For the present purposes of this Annex that issue can be postponed. It is sufficient here to define some "object" that produces a constant material force on the SP whatever the speed u of the SP relative to the aether. Suppose that such object is a small "active box" that moves closely behind the SP maintaining at all times the same velocity as the SP. Let r(v) be the redistribution created by the box along the semi direction X in which both the box and the SP are moving relative to the aether:
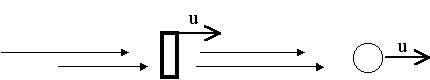 Fig[M-10]
Fig[M-10]
ru(v) will here represent the 1-D redistribution made by the box in the speeds of the pertinent aetherinos that are those that travel with a velocity along the semi direction +X. The speeds v are relative to the box (and hence relative to the SP). (Although the box will in general be accelerating with the SP, if box and SP are close enough it can be approximated that the significant aetherinos reach the SP at the same relative speed at which they departed the box).
The aetherinos entering the box from its back are those of the undisturbed aether and have therefore the same speed distribution of the aetherinos that would reach the SP from its back in the above case of no material force. The exact form of ru(v) may depend on the speed u of the box through the aether but this is unimportant. It will ad hoc be supposed that, whatever u, the box behaves as follows: (though the following features might not seem very plausible to describe a real material force it must not be forgotten that the box implements only an ad hoc theoretical constant force to allow for the calculus).
- 1) the total number of aetherinos entering the box from its back in unit time is the same as the total number of aetherinos exiting the box from its front in unit time. This implies:
![]() [M-11]
[M-11]
- 2) for a given aetherino speed v it will happen that either ru(v) > 0 (i.e. a higher number of aetherinos of speed v exits the box from its front than those of speed v arriving to its back) or ru(v) < 0 (i.e. a smaller number of aetherinos of speed v exits the box from its front than those of speed v arriving to its back). This will allow to assume that:
-3) The average speed of the aetherinos exiting the box (in unit time) from its front is different from the average speed of the aetherinos entering the box (in unit time) from its back. This is what allows the SP to suffer a net aetherinical force from the box, either repulsive or attractive. It will be supposed that, whatever the speed u of the box and the SP relative to the aether, the "internal mechanism" of the box is such that the following integral takes the same constant value F:
![]() [M-12]
[M-12]
The factor 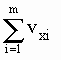 of [M-5] giving the sum of the x-components of the velocities (referred
to the frame S of the aether) of the m aetherinos colliding with the SP can therefore
be expressed, in this case of material force, as:
of [M-5] giving the sum of the x-components of the velocities (referred
to the frame S of the aether) of the m aetherinos colliding with the SP can therefore
be expressed, in this case of material force, as:
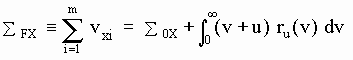 [M-14]
[M-14]
that takes into account that the aetherinos of direction X and speed v relative to the box have an x velocity component v+u relative to the aether frame. [M-14] expresses that now the sum of x components is obtained adding to the sum S0X (given in [M-7b] for the case of no material force and no redistributing box) the x-components of the aetherinos emerging from the front of the box and subtracting the x-components of the aetherinos entering the back of the box, or what is the same, adding the integral that appears in [M-14]. (Remember that ru(v) is negative when there is a deficit of aetherinos of speed +v relative to the box).
The Eq[M-14] can be developed as follows:
![]() [M-14b]
[M-14b]
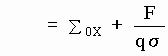 [M-14c]
[M-14c]
where the first integral of [M-14b] has been expressed according to [M-12] and where the second integral of [M-14b] is zero due to [M-11].
The acceleration of the SP takes now the form:
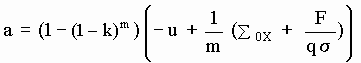 [M-15]
[M-15]
where m is "equal" to the Y of [M-6b] , S0X is given in [M-7b], F is the constant material force, q is the (unimportant) constant used in the definition of the elementary aetherinical impulse (i = q.vR) and s is the geometrical cross section of the SP.
After dimensionally "repairing" [M-15] similarly to what was done above it takes the form:
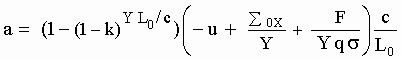 [M-15b]
[M-15b]
[M-15b] is interpreted to give, for the Ideal Observer, the acceleration of a Simple Particle moving through the aether with speed u, in presence of an aetherinical material force F acting on the SP in the same direction as u. The acceleration is now due to both the material force and to the aether drag force.
The question is now: what is the acceleration observed by the official observer OO?. As has been said many times in this work, it is assumed that this observer OO detects no deceleration of "free" particles (subject only to the aether drag force) because his real clocks decelerate at the same rate. But he will observe an acceleration when there is a material force acting as well.
to be continued